개요
SVD라는 건 무엇인지 알아보자.
SVD란?
지금까지 행렬을 분해하는 방법으로서 한 가지를 배웠는데, 그것은 바로 eigendecomposition이다.
eigendecomposition의 수식은 A = VΛV^-1로 나타낼 수 있었다.
그리고 수식에 대한 이해를 해보자면 선형 변환 A를 3개의 layer로 쪼개는데 V는 벡터를 회전시키고, Λ는 벡터를 scaling하는 역할을 맡는다. (V^-1도 마찬가지로 회전이지만 반대 방향으로 회전하는 것이다.)
이런 행렬 분해법인 EVD는 사용하기 위해서 약간의 제약 조건들이 있었다.
- A가 Diagonalizable 해야 eigendecomposition을 가질 수 있다.
- A는 무조건 square matrix여야 한다.
- V는 무조건 invertible 해야 한다.
- + symmetric해야만 A = QΛQ^-1를 사용할 수 있다.
이런 제약 조건들 없이 행렬 분해를 도와주는 녀석이 바로 SVD이다.
SVD는 정보량의 크기(σ)에 따라 A를 여러 layer로 쪼개주는 역할을 한다.
SVD는
- A가 직사각행렬이어도 정의된다.
- 그러므로 A가 diagonalizable하지 않아도 된다.
- V가 invertible하지 않아도 된다.
즉, SVD는 어떤 행렬이든 존재한다.
그리고 SVD가 묻는 것은 무엇이냐?
"직교하는 벡터 집합(V)에 대하여,
선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게 만드는
그 직교 벡터 집합(U)은 무엇이고
변환 후의 결과는 무엇인가?"
SVD의 형태
수식을 먼저 알아보자.
A = UΣV^T
이번에는 각각 요소들의 shape이 어떻게 되는지 이미지로 확인해보자.
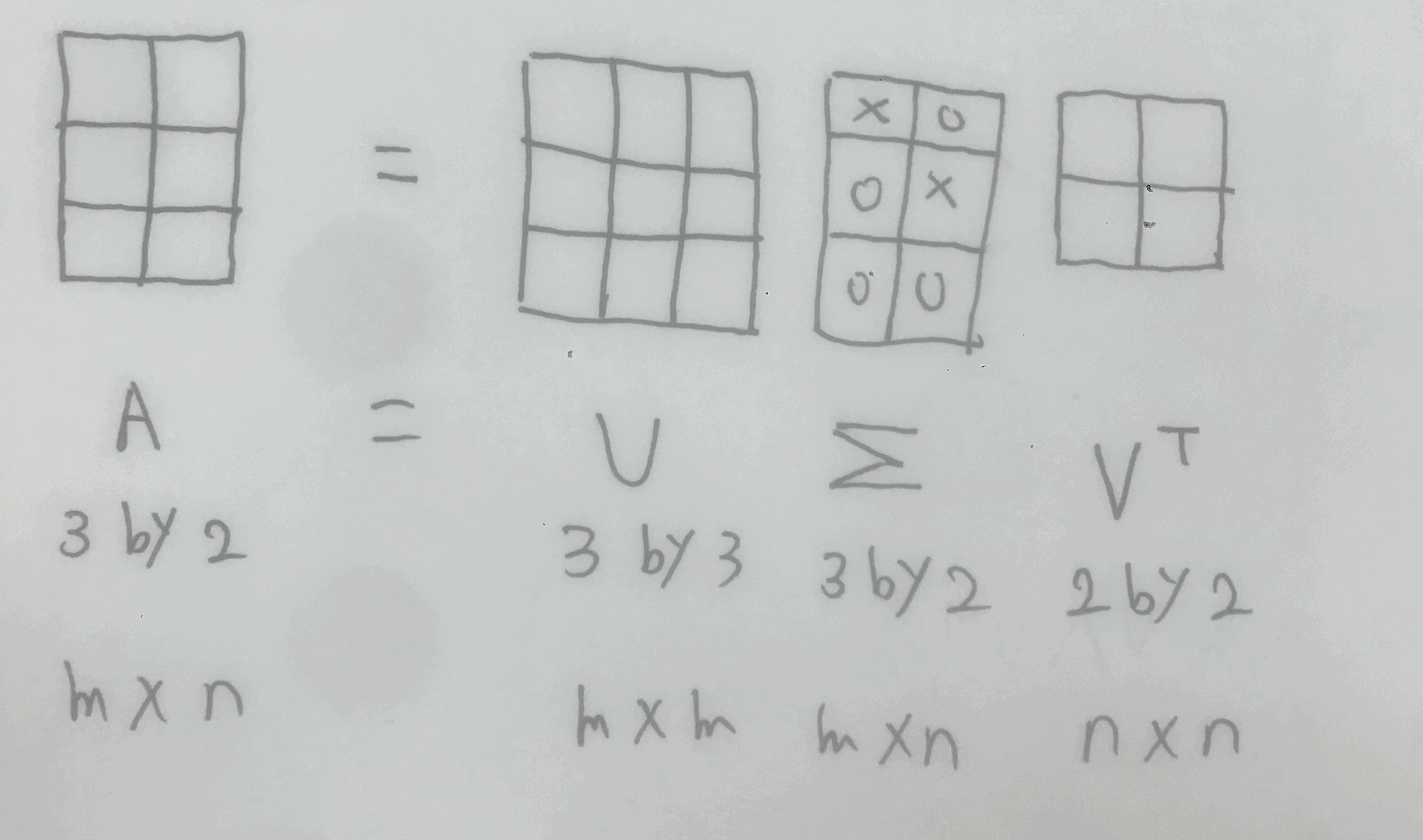
이번에는 이 식의 요소들인 UΣV^T에 대해 하나씩 알아보자.
다만 Ax = UΣV^Tx이어서 벡터 x에 선형 변환을 일으킬 때면, 연산이 오른쪽부터 일어나기 때문에
맨 오른쪽에 있는 V^T
부터 설명을 시작하겠다.
+ 시작 전 중요한 것이 하나 있다.
우리는 A를 A^TA and AA^T로 사용한다.
1. V^T
V^T는 orthogonal matrix이다.
V는 A^TA의 eigenvector들을 column으로 쌓은 matrix이다.
그럼 즉, V^T는 그 V를 transpose하여 A^TA의 eigenvector들을 row로 쌓은 matrix이다.
2. Σ
Σ는 diagonal matrix이다.
ㄴ> eigendecomposition의 D를 떠올리면 편하다.
다만, Σ는 다른 점이 있다.우리는 A가 아닌 A^TA로 사용하고 있다.
eigendecomposition에서 D의 요소로 람다가 들어갔는데 이번에는 Σ의 요소로 σ가 사용되고 있다.
간단하게 설명하면,람다는 람다이지만 σ는 A^TA의 eigenvalue에 square root를 씌운 형태이다.그니까 람다에 루트를 씌우면 σ 이렇게 시그마로 표현이 되는데그걸 모은 게 Σ라는 거다.
즉,σ는 A^TA의 eigenvalue의 square root, λ^1/2이다. 이를 singular value라고 부른다!
Σ는 σ들을 diagonal하게 정리해놓은 matrix이다.
다만, D와는 달리 Σ는 정사각형이 아니기에 diagonal matrix라고 정의할 수 없다.
안의 내용도 조금은 다르다.

이런 식으로, singular value들이 있는 행이나 열까지 diagonal하게 정리한다음 나머지는 모두 0으로 채운다.
이게 Σ의 형태이다.
이것으로 알 수 있는 것은
eigenvalue가 나올 수 있는 최대 개수는 A(m by n)의 shape에서 얻을 수 있고 n개라는 걸 알 수 있다!
3. UU는 orthogonal matrix이다.
U는 column space of A의 orthonormal한 basis가 column으로 쌓여있는 matrix이다.
이 orthonormal한 basis들은 당연하게도 A의 차원만큼 존재해야 한다!
우리가 가정하는 A가 5 by 3이면, dim(A) = 5이므로 U도 5차원이어야 한다!
'자연어 처리 과정' 카테고리의 다른 글
| 경사하강법 (0) | 2022.11.28 |
|---|---|
| determinant가 0이라는 것의 의미는? (0) | 2022.11.25 |
| Change of basis의 이해 (0) | 2022.11.23 |
| Eigendecomposition의 기하학적 이해 (0) | 2022.11.23 |
| Gram-schmidt process를 알아보자. (0) | 2022.11.19 |



