개요
개인적으로 정말로 정말로 정말로 이해하기 힘들었던
linear transformation에 의한 change of basis를 알아보기로 하자.
일단 선형 변환 A가 벡터 x를 통과해서 벡터 b가 된다는(Ax=b) 이 말을 제대로 이해를 할 필요가 있다.
나는 이게 무슨 말인지 알고 있는 줄 알고 넘어갔는데, 알고 보니 그냥 의미를 아예 모르는 거였다.
그래서 change of basis를 이해하는 데 엄청 애를 먹었던 것 같다.
물론, 100%로 change of basis, linear transformation을 이해했다고는 못하겠다.
그냥 이제야 좀 무슨 말인지 알겠다는 말이다.
밑바탕이 될만한 지식
그럼 Ax=b라는 게 도대체 뭘까?
선형대수학을 시작할 때 알려준 내용인 것 같은데 지금까지 아는 척만하고
하나도 제대로 이해하지 못하고 있었던 나도 참 대단한 것 같다.
우리는 현재 Ax=b 꼴의 선형 변환에서 A를 matrix로 한정지어 보고 있다.
A는 듣기로는 뭐 뉴럴 네트워크가 될 수도 있고 다양하다고 한다.
그러니까, Ax=b가 뭐냐?
A를 matrix로 봤을 때, A라는 matrix가 벡터 x의 값에 변화를 일으켜서 벡터 b로 만든다는 의미를 지니는 수식이다.
만약 A가 뉴럴 네트워크라면 matrix 때와는 조금 다른 의미를 지니겠지만, 결국 A에 의해 벡터 x를 변환시켜 b를 얻는다는 건 똑같을 것이다.
그런데 이 변환의 결과가 선형이라서 선형 변환 즉, linear transformation인 것이다.
Change of basis란?
linear transformation에 대한 이해가 끝났다면, change of basis가 무엇인지 알 시간이다.
동시에 일어나는 것이기 때문에, 내 생각으로는 linear transformation이나 change of basis나 같은 말이라고 볼 수도 있을 것 같다.
하지만 나는 linear transformation이 일어나서 change of basis가 일어난다고 보고 싶기 때문에
linear transformation을 설명한 후에 change of basis를 설명하려고 한다.
그래서 change of basis가 뭐냐?
우리는 A에 의해 linear transformation이 일어난다.
그러니까 선형 변환 A에 의해서 벡터 x가 변환을 한다.
우리는 A를 matrix에 국한지어 공부하고 있고 벡터를 공부하고 있기 때문에
우리가 현재 공부하는 세상에서 Ax=b는 좌표의 변환이다.
그러니까 정리해서 말하면, Ax=b를 통해 벡터 x의 좌표가 변한다는 거다.
여기서 중요한 건 도대체 뭐가 어떻게 변하냐는 것이다.
가정을 하고 시작하겠다.
1. 우리의 원래 세상에서는 basis가 standard basis이다.
그래서 basis i, j가 있다.
i = [1,0], j = [0,1]이다.
2. new basis가 축인 세상에는 basis a,b가 있다.
a = [2,1], b = [1,2]이다.
3. 원래 세상에서 [-3,0]지점에 점을 하나 찍었다.
그리고 이 지점의 좌표를 담은 벡터를 vector v라고 하겠다.
Q. 그럼 new basis가 축인 세상에서는 [-3,0]이 어디일까?
이제 시작하자.
우리는 현재 new basis가 축인 세상에서는 원래 세상의 [-3,0]이 어디일까를 찾으려고 한다.
그럼 일단 우리의 선형 변환 식을 가져와보자.
Ax = b이다.
어떻게 알 수 있을까?
바로 선형 변환을 통해 알 수가 있다!
값을 넣기 전에, 값을 넣을 때 도움이 되는 설명! (중요!!!!)
이 부분은 내가 선형 변환을 이해하는 데에 있어서, change of basis를 이해하는 데에 있어서 나에게 엄청난 도움이 된 팁이다.
이렇게 이해하자.
1. new basis 세상의 좌표를 원래 basis에서 나타내고 싶다!
A에는 항상 new basis의 matrix가 들어간다.
x에는 new basis 세상에서 해당 점의 좌표가 어디인지 x에 넣으면 된다.
그럼 b에는 new basis 세상의 좌표가 주어진 원래 basis 세상에서는 어디에 나타나는지 알 수 있다!
그러니까, new basis 세상에서 x를 결합하면 원래 basis 세상의 좌표가 나타난다!
2. 원래 basis 세상의 좌표를 new basis 세상에서 나타내고 싶다!
위와는 달리,
basis 세상에서 new basis 세상으로 변환하는 거니까 A에 역행렬을 취해준다.
그러니까 Ax=b에서 A 자리에 new basis의 matrix에 역행렬을 취해준 형태가 들어간다.
그리고 new basis의 matrix의 역행렬을 취해준 형태를 standard basis의 matrix라고 생각해주면 된다!
그럼 x에는 어떤 좌표가 들어가는 것이냐?
원래 basis 세상에서 어떤 좌표에 나타나는지를 x에 넣으면 된다.
그럼 b에는 원래 basis 세상의 좌표가 new basis 세상에서는 어디에 나타나는지 알 수 있다!
이제 값을 넣어 문제를 해결해보자! (중요!!!!!)
원래 basis가 축인 세상에서의 좌표가 주어졌다.
그것이 vector v이고 좌표는 [-3,0]이다.
그리고 구하려는 것은 이 vector v를 a,b가 basis인 세상에서 나타내려면 어디에 나타내야 하는지 좌표를 구하는 것이다!
그럼 i,j 세상에서 a,b 세상으로 들어가서 좌표를 알아내야 한다.
식이 어떻게 될까?
Ax=b이고,
A에는 new basis a,b가 column으로 쌓여있다.
x가 바로 new basis 세상에서 [-3,0]을 나타낸 좌표인데, 우리는 지금 이것을 찾으려고 하기에 x로 둔다.
b가 바로 new basis 세상의 x좌표를 원래 basis 세상에서 나타냈을 때의 좌표인데 이것이 vector v이다.
계산 과정은 이미지로 보자!
(Ax=b 꼴이다.)
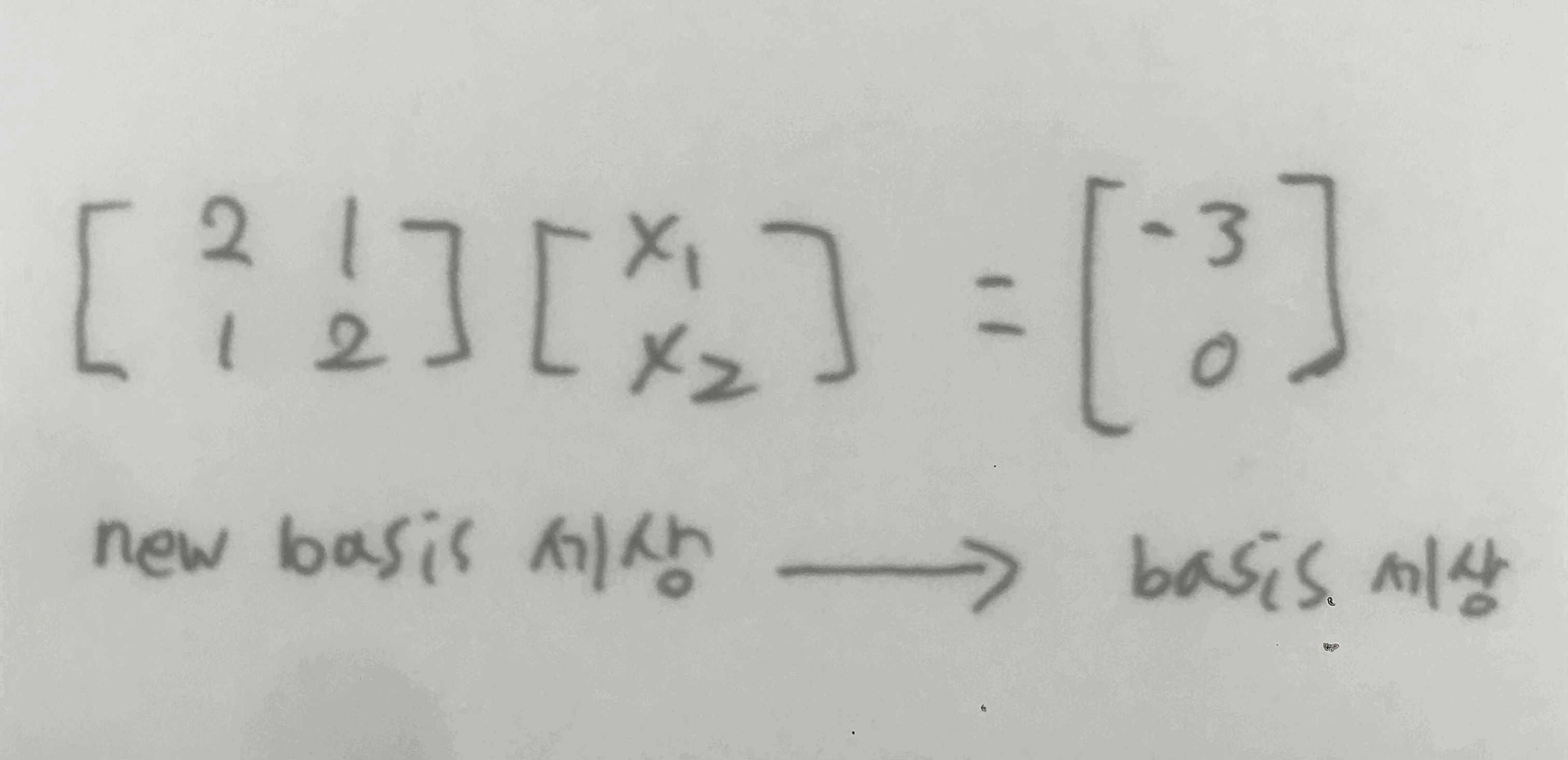

해를 구하는 건 그냥 Linear system을 풀면 된다!


이제 저 벡터값을 다시 식에 집어넣자.
다시 Ax=b 꼴이다.


이렇게 이해하면 된다.

원래 basis 세상에서 빨간 벡터 v는 (-3, 0)으로 나타난다.
하지만 new basis 세상에서는 빨간 벡터 v는 우리가 구한 (-2,1)로 나타나는 걸 볼 수 있다.
그럼 원래 세상에서 new basis의 세상으로 가려면 어떻게 해야할까?
만약에 new basis상에서의 좌표만 주어져있다고 하자.
그리고 그 좌표가 원래 basis 상에서는 어디인지 물어본다고 해보자.
Q. i,j와 a,b basis는 그대로 유지하고
주어진 vector v는 a,b 상에서 [-2,1]로 나타난다고 한다.
그럼 i,j 상에서 vector v를 나타내라!
간단하다.
이번에는 matrix에 역행렬만 취해주면 된다!
그리고 matrix에 역행렬을 취해준 게 원래 basis라고 생각하면 된다.
이번에는 식은 그림으로 나타내고, 계산은 코드로 나타내겠다.


이렇게 식을 세웠으니 계산을 해보자.
이번에는 역행렬이 있으니까 역행렬을 먼저 계산해주자.
코드로 편하게 계산해보자.

역행렬을 구했으니 위에서처럼 linear system을 풀어 해를 구해주면 된다!
그 해는?
원래 basis 세상에서 new basis 세상의 [-2,1]을 나타내려면 어디에 점을 찍어야 하는지 말해주는 벡터이다!

그럼 해는?

이미 위에서 알고 있었지만, (-3,0)이 나온다!
이를 활용해서 다른 basis 세상으로 이동을 한 다음, 그 세상에서 rotation, scaling, shearing 등의 선형 변환을 한 후
다시 원래의 basis 세상으로 돌아와서 좌표를 확인해볼 수도 있다!
이걸 이해하는 데 정말 오랜 시간이 걸렸다...
그래도 이제는 어느 정도 무슨 말인지 이해가 된다니 정말 다행이다.
'자연어 처리 과정' 카테고리의 다른 글
| determinant가 0이라는 것의 의미는? (0) | 2022.11.25 |
|---|---|
| SVD의 이해 (0) | 2022.11.24 |
| Eigendecomposition의 기하학적 이해 (0) | 2022.11.23 |
| Gram-schmidt process를 알아보자. (0) | 2022.11.19 |
| onto와 one-to-one (0) | 2022.11.18 |



