개요
Eigendecompostion이 뭔지 조금 살펴보고
Eigendecompostion을 기하학적으로 이해해보자.
Eigendecompostion? 선형 변환과 함께 이해하자.
Linear transformatioin 즉, 선형 변환 A를 고윳값으로 분해를 해볼 수 있다는 것이 바로 eigendecompostion이 의미하는 바이다.
일단 선형 변환의 의미를 잘 알아야 기하학적 해석에서도 이해를 할 수 있을 것 같다.
나는 선형 변환과 change of basis를 제대로 이해하지 못한 상태에서 eigendecompostion에 대해 설명을 들었다.
이해하기가 개인적으로 너무 어려웠다. 사실 지금도 제대로 이해했는지 확실하지는 않다...
가볍게 선형 변환을 짚고 넘어가보자면, Ax=b꼴이 있다고 가정하자.
그럼 여기에서 A가 벡터 x를 변환시켜서 b로 만든다는 이야기이다.
여기에 basis를 첨가해서 이야기해보자면,
A가 [2,1], [0,1]이라고 해보자. 그리고 x가 [3,0]이라고 해보자.
이 말은 무엇이냐?
basis가 [2,1], [0,1]일 때 즉, 그래프의 축이 [2,1], [0,1]일 때의 [3,0]이
standard basis(원래 그래프)에서는 b라는 것이다.
선형 결합으로 b 점을 구해보면 [2,1], [0,1] 세상에서 [3,0]은 사실 원래 세상에서는 [6,3]이라는 걸 알 수 있다!
이렇게 선형 변환을 eigendecompostion과 함께 설명을 하는 이유는 기하학적으로 eigendecompostion을 이해하는 데에 선형 변환에 대한 이해가 꼭 필요하기 때문이다.
eigendecompostion의 수식
우리는 고윳값과 고유 벡터에 대해 공부하면서 Ax = λx라는 수식을 얻을 수 있었다.
이 의미는 간단하다. 선형 변환 A를 거쳤는데, 변화된 벡터가 방향은 변하지 않고 λ만큼 scaling만 됐다는 이야기이다.
우리는 이 수식으로부터 eigendecomposition의 수식인 A = VΛV^-1을 얻을 수 있었다.
이 수식의 의미는 무엇이냐?
여기서 선형 변환이 중요하다.
선형 변환 A는 원래 이런 벡터를
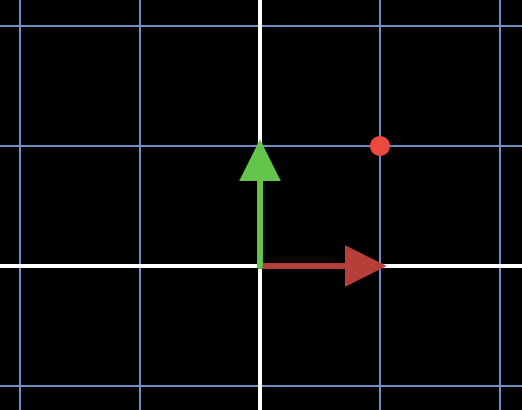
이렇게 변환시킨다. 즉, basis를 바꿔버리면서 그래프의 모양이 아예 바뀌게 된다.

이 위의 사진이 바로 A의 결과인데,
A는 바로 변환의 결과가 나타나니까, eigendecomposition을 통하면 이 변환을 3가지 과정으로 쪼개서 볼 수 있다는 것이다.
그것이 바로, A = VΛV^-1의 의미이다.
V는 방향값만 가지고 있고, eigenvector들을 orthogonal하게 만들어버리면 이는 rotation matrix이기 때문에
V는 돌리는 역할을 맡고 있다.
Λ는 크기값을 가지고 있으니까, scaling 즉, 벡터를 늘리는 역할을 맡고 있다.
V^-1은 역시 회전을 해주는 역할인데 V^-1이므로 반대로 돌려주는 역할이다.
착각하면 안 되는 중요한 점은 계산 순서는 바로 V(Λ(V^-1x))라는 것이다!
그러니까, A는 벡터를
1. 반대로 돌리고
2. 늘려주고
3. 다시 원래대로 돌려준다!
이렇게 볼 수 있다는 것이다!
기하학적으로 eigendecomposition을 살펴보자.
지금까지 eigendecomposition을 수식으로 이해해봤으니
그 돌리고 늘리고 돌리는 과정을 그림으로만 이해하면 된다!
우선, 몇 가지 가정을 하겠다.
eigenvalue는 -1과 2
eigenvector는 [3,1]과 [-2,1]
초기의 x를 [4,3]이라고 하겠다.
우리가 선형 변환 A를 하는 순서는 V(Λ(V^-1x))임을 기억하자.
1. V^-1x
이를 여기에서 나올 output을 y라고 생각하자.
그럼 우리는 y = V^-1x를 얻을 수 있다.
그리고 이미 우리가 V와 x를 알고 있다고 가정했으므로 계산을 하기 쉽게 V^-1를 없애기 위해 V를 곱해주자.
결과적으로, Vy = x를 얻을 수 있다.
이를 값을 대입해서 적어보자면,
[3,1],[-2,1] y = [4,3]이다.
이게 무슨 의미냐?
basis가 eigenvector인 즉, basis가 [3,1]과 [-2,1]인 세상에서의 y점은
원래 세상에서는 [4,3]이라는 것이다.
그러니까, [4,3]이 eigenvector가 basis인 세상에서는 y라는 것이다.
그럼 y를 어떻게 구하나?
그냥 저 linear system을 풀면 된다!
그럼 결과로 y1 = 2, y2 = 1이 나오고, [3,1],[-2,1] @ [2,1] = [4,3]인 것이다.
이제 저 식을 말로 정리할 수 있다.
우리는 지금 돌리는 과정을 x에다가 해주고 있다, V^-1x이니까!
x는 [4,3]이었고, 우리는 이 x를 eigenvector가 basis인 세상으로 돌리려고 한다.
그런데 그때 x는, 그러니까 돌렸을 때, eigenvector가 basis인 세상이 되었을 때 x는 어디에 있을까?
그게 바로 y인 것이다.
V^-1x를 통해서 선형 변환을 일으켰고 V^-1는 방향값만 갖고 있기 때문에 회전만 일어난다.
이를 통해 얻은 식이 [3,1],[-2,1] @ [2,1] = [4,3]이며, 이 식은 무엇을 의미한다?
eigenvector [3,1]과 [-2,1]의 세상에서 원래 세상의 [4,3]을 표현하면 [2,1]이다!
왜 이걸 표현하냐?
x 벡터를 V^-1와의 선형 결합의 결과로서 회전을 시켜야 하니까!

사진을 보면 더 이해할 수 있을 것이다.
점이 찍혀있는 부분이 basis가 [1,0], [0,1]일 때, 그러니까 원래 세상일 때 x였던 [4,3]이다!
그런데 선형 변환 V^-1을 통하면 basis가 eigenvector로 변하고 원래 basis에서 [4,3]이었던 x는
basis가 eigenvector로 변한 세상에서는 [2,1]로 표현된다는 것이다!
2. Λ(y), (우리가 구한 output이 x를 돌린 결과인 y였으니까, y로 대체해서 넣은 것이다.)
이제는 다음 단계인 늘리기를 할 차례이다.
이번에는 선형 변환이 Λ이고, 이는 eigenvalue이다.
따라서 x에 scaling만 해줄 것이라고 예상할 수 있다.
그러니까 이번 단계에서는 x 벡터의 크기만 조정해준다는 것이다!
되게 간단하다.
그냥 현재 우리가 가지고 있는 벡터인 y에다가, eigenvalue값이 diagonal하게 담겨있는 Λ matrix를 곱해주면 된다!
diagonal하기 때문에 그냥 상수배를 하는 느낌이다.
계산을 하기 전에, 이번 단계의 결과값을 z라고 생각하자.
그럼 z = Λy이다.
초기의 가정에 따라, 우리는 eigenvalue값으로 -1과 2를 가지고 있다.
우리의 y는 [2,1]이므로 곱해주면, [-2, 2]가 나온다는 것을 알 수 있다.
이게 끝이다.
z = [-2, 2]이다.

위에 있던 사진과 비교하면, 선형 변환에 따른 scaling에 의해 벡터가 변했음을 확인할 수 있다.
그래서 결과로 eigenvector 세상의 [2,1](y값)을 가리키고 있었지만
scaling을 통해 이제는 [-2,2](z값)를 가리키고 있다!
3. V(z), 이제는 원래대로 돌려줄 시간!
이제 다시 선형 변환 V로 돌아왔다.
선형 변환이 V라는 건 뭐였나?
그건 바로 벡터에 회전을 시켜주는 것이었다!
처음에 했던 회전은 V^-1이었으므로 이번에는 다시 원래대로 회전을 시킬 차례이다.
다시 원래대로 회전을 시킨다는 게 무엇이냐?
처음의 회전을 통해 우리는 원래의 basis 세상에서 eigenvector가 basis인 세상으로 벡터를 변환시켰다.
그리고 그 벡터를 람다로 scaling시켜서 길이를 변환시켰다. (여기까지도 eigenvector의 세상에서 일어나는 변화이다.)
이제는 eigenvector가 basis인 세상에서 변환을 모두 끝냈으니, 다시 원래 basis 세상으로 벡터를 변환시켜줄(돌려보내줄) 차례이다!
eigenvalue 값으로 우리는 y의 점이었던 [2,1]을 곱해주어 [-2,2]로 변환시켰다.
뭘 알아보는 거냐?
원래 basis를 가지는 세상에서 eigenvector 세상의 [-2,2]를 표현하려면 어디일까를 묻는 것이다!
즉, eigenvector 세상의 [-2,2]를 원래의 basis 세상에서 표현해보면 어디에 점을 찍으면 되는가이다!
그럼 수식이 어떻게 나올까?
일단 현재 Ax = Vz인 상황이다.
왜?
이 마지막 단계만 거치면 결국 선형 변환 A가 x를 통과한 것과 결과가 같으니까!
그리고 Vz를 계산하기 위한 식을 적게 되면
위에서 V^-1을 했을 때와 똑같은 형식으로 나타낼 수 있는 것이다.
eigenvector의 세상의 [-2, 2]는 원래의 세상에서 어디인지 확인해보는 것이니까,
[v1, v2] @ [-2,2] = eigenvector가 basis인 그래프의 [-2,2]를 원래 세상에서 표현하는 좌표값
그럼 여기에 값을 넣어보면
[3,1], [-2,1] @ [-2,2]이다.
이를 선형 결합하면?
[-10, 0]이 나온다.
이 [-10, 0]이 무엇이냐?
원래 세상에서는 eigenvector 세상의 [-2, 2]가 [-10, 0]에서 표현된다는 것이다!
그러니까, 늘리고 돌린 벡터를 다시 원래 세상으로 돌려보니 그 점이 [-10, 0]이더라, 라는 의미이다!

그림을 보면 더 이해가 될 수 있다.
저기 점이 찍힌 부분이 eigenvector가 basis인 세상에서의 z이고 그 좌표는 [-2, 2]이다.
[-2,2]는 어떻게 얻었느냐? 그것은 바로 위의 두 가지 과정 (선형 변환 V^-1과 Λ를 통해 얻었다.)
그런데 이제는 반대로 돌려줄 시간이었으니까, eigenvector의 세상에서 [-2,2]이었던 부분을
원래 세상에서 표현하려면 어디였는지 알고 싶은 것이다.
그것을 아는 방법은 eigenvector와 z의 선형 결합이었고, 그 결과값으로 [-10, 0]을 얻었다.
결국, eigenvector가 basis인 세상의 [-2,2]인 점은 원래 basis를 가진 세상에서는 [-10,0]이었다는 것이다!
그래프의 오른쪽 면에 남아있는 점은 초기에 벡터가 있었던 곳이고, 선형 변환 후에 벡터가 어떻게 변환되었는지(얼마나 돌았고, 늘었고, 돌았는지) 나타내주기 위해서 남겨둔 것 같다.
밑의 블로그에서 도움을 받았습니다.
https://angeloyeo.github.io/2019/07/15/Matrix_as_Linear_Transformation.html
행렬과 선형변환 - 공돌이의 수학정리노트
angeloyeo.github.io
'자연어 처리 과정' 카테고리의 다른 글
| SVD의 이해 (0) | 2022.11.24 |
|---|---|
| Change of basis의 이해 (0) | 2022.11.23 |
| Gram-schmidt process를 알아보자. (0) | 2022.11.19 |
| onto와 one-to-one (0) | 2022.11.18 |
| Orthogonal projection을 위한 점을 찾는 수식 (0) | 2022.11.17 |



