Drawing computation graphs
현재까지의 과정을 통해 알아보았던 task로는 linear regression과 logistic regression이 존재했다.
이번에는 그 모델들이 prediction을 만드는 과정과 prediction이 loss function에 입력되는 과정을 computation graph로 표현해보고자 한다.
이 과정을 통해 먼저 모델들의 forward pass 과정을 이해해보자.
Computation graph of Linear regression
먼저 linear regression의 가설을 만들기 위한 parameter로는 θ만이 존재한다고 가정한다.
그리고 data는 2개가 존재해서 x1, x2가 존재한다고 가정한다.
그렇다면 linear regression의 가설을 만들기 위한 요소로는 2차원 vector x와 2차원 parameter vector θ가 존재하는 상황이다.
일반적으로 linear regression 모델의 가설은 아래와 같은 모양새를 따른다.

먼저 scalar value 단위로 linear regression w/ MSE를 computation graph로 나타내면 아래와 같다.

위를 한 줄의 식으로 나타내면 아래와 같다.

이번에는 좀 더 간결하게 x와 θ를 vector로 취급하고 computation graph를 그려보자.

Computation graph of logistic regression
Linear regression을 위해 가정했던 상황을 그대로 사용한다.
그리고 그 가정 상황에서 task만 binary classification으로 변경하고자 한다.
Logistic regression은 θ와 data x를 이용해서 logit 값을 구한 후 softmax를 통해 그 값들을 총합 1의 확률값으로 만들어 prediction을 만든다.
위와 같은 과정을 통해 만들어지는 가설과 NLL에 그 가설이 적용되는 과정까지 computation graph로 나타내보자면 아래와 같다고 할 수 있다.

위를 식으로 표현하게 되면 아래와 같다.

이때, data vector x의 shape은 (2 x 1)이고, θy의 vector shape 또한 (2 x 1)이다.
따라서, vector 형태로 둘을 취급하고 간결하게 computation graph를 나타내면 아래와 같다.

From computation graph to neural net diagram and forward pass
위에서 표현했던 logistic regression의 computation graph를 neural net의 형태로 간결하게 표현해보자면 아래와 같이 표현할 수 있다.

그리고 이를 diagram 형식으로 표현하면 아래와 같다.
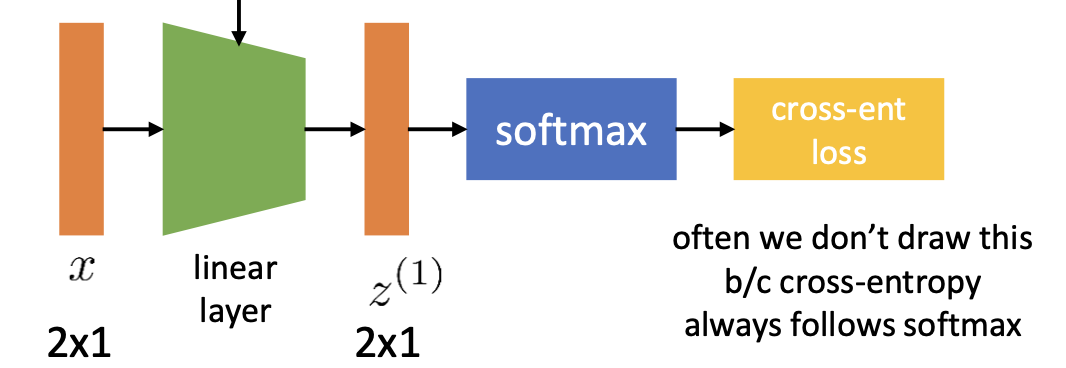
지금까지의 과정을 통해 우리는 linear regression과 logistic regression task에서 어떤 과정을 거쳐서 prediction을 만드는지 알아보았고 그 prediction을 loss function의 입력으로 집어넣는 과정까지를 한 줄의 일련의 과정으로 나타냈다.
위를 다른 말로 표현해보자면, 우리는 현재 linear regression과 logistic regression의 forward pass가 대충 어떤 흐름인지 알게 되었다.
다만, 완성된 forward pass라고는 할 수 없다.
그렇기 때문에 이제부터는 완성된 simplified forward pass를 묘사하기 위해 필요한 과정을 알아보자.
More features
만약 우리가 logistic regression task를 진행하고 있고, linear classifier를 통해 아래의 data들을 classification 한다고 생각해보자.
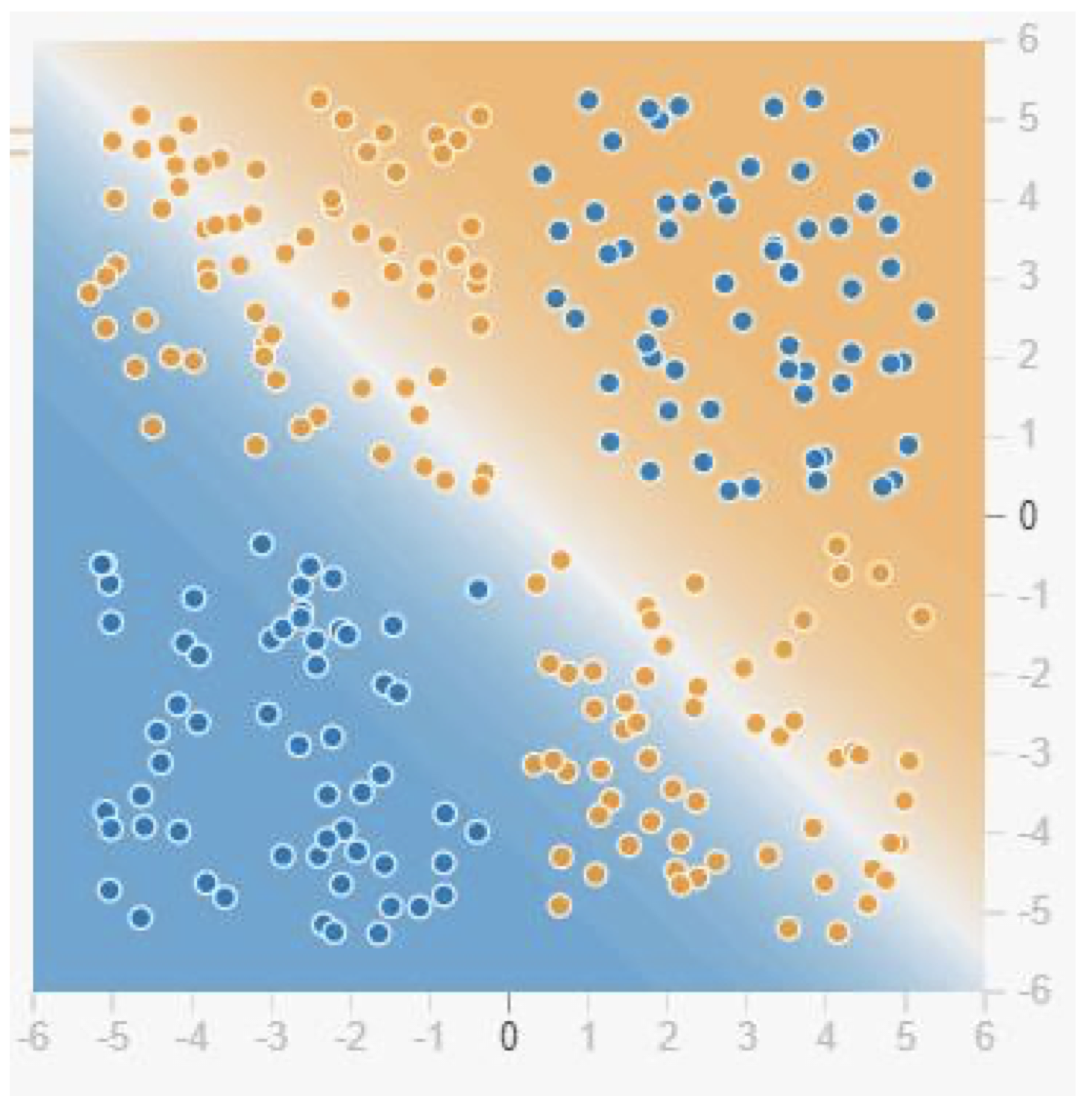
Data point들의 분포 상황으로 보았을 때, 우리는 linear classifier로 제대로 classification을 해낼 수가 없다.
그렇기 때문에 우리는 x1,x2뿐만 아니라, x21,x22,x1∗x2와 같은 추가 feature들을 필요로 하게 된다.
그러한 추가 feature들이 존재하게 된다면 우리는 위의 data point들을 잘 classification 할 수 있을 것이다.
이러한 추가 feature들을 만드는 일을 하는 layer가 바로 linear layer이다. Linear layer에 존재하는 weight의 shape을 조절함으로써 우리의 input에 추가 feature들을 넣는 것이다.
Learning the features
모델이 더 좋은 표현력을 가질 수 있도록 우리는 추가적으로 feature를 넣어주었다.
그렇다면 그 feature들은 input과 만나 learned가 되었을 것인데, 그 learned feature들을 어떻게 representation 해줄 수 있을까?
즉, feature들과 input이 만나 learned된 feature들의 값들은 굉장히 다양할 것이다.
이를 어떻게 표현해주는 것이 좋을까?
Activation functions 중 하나인 sigmoid를 사용하여 learned feature 값을 0 ~ 1 사이의 값으로 표현해주자.

Draw this
이제 위와 같은 과정을 다시 neural net의 형태로 표현해보자면 아래와 같다.

이렇게 activation function까지 추가를 하고 나면, 우리는 logistic regression의 simplified forward pass를 한눈에 살펴볼 수 있게 되었다.
Logistic regression은 위와 같은 과정이 반복을 이루면서 층을 쌓는다.

Why activation function?
Layer들이 쌓인 것들을 보면 사이사이에 activation function인 sigmoid가 계속해서 들어가 있는 것을 알 수 있다.
위에서는 activation function을 넣어줌으로써 learned feature를 representation 하는 것이라고 말했다.
Activation function을 넣어주는 이유에 대해 좀 더 자세히 해보자면, 우리의 function에 비선형성을 넣어주기 위함이라고 할 수 있다.
만약, 우리가 linear layer를 계속 쌓는다고 해보자. 그렇다면 아래와 같이 계속해서 선형 변환이 쌓이게 된다.
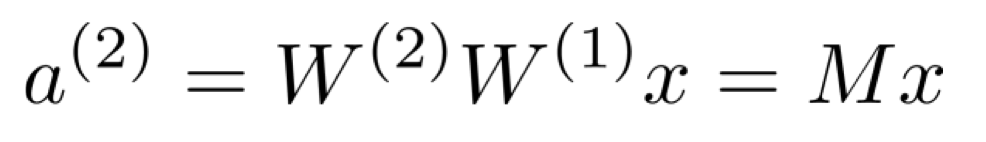
하지만 그러한 수많은 linear layers에 의한 선형 변환은 결국 1개의 선형 변환으로, 1개의 linear layer로 나타낼 수 있게 된다.
그렇기 때문에 대신 linear layer와 함께 비선형성을 같이 쌓아줌으로써 우리는 무엇이든 representation 할 수 있게 되는 것이다.
Training neural nets with chain rule
우리는 위에서 이루어졌던 과정을 통해 logistic regression task 상황에서 어떻게 neural net을 이루는 layer가 쌓이고, forward pass가 어떻게 되는지 알 수 있었다.
쉽게 말하자면, 우리는 neural net를 구성했다고 말할 수 있다.
그렇다면 이제 우리는 그 neural net을 training 시키기만 하면 된다.
어떻게 그 neural net을 training 시킬 수 있을까?
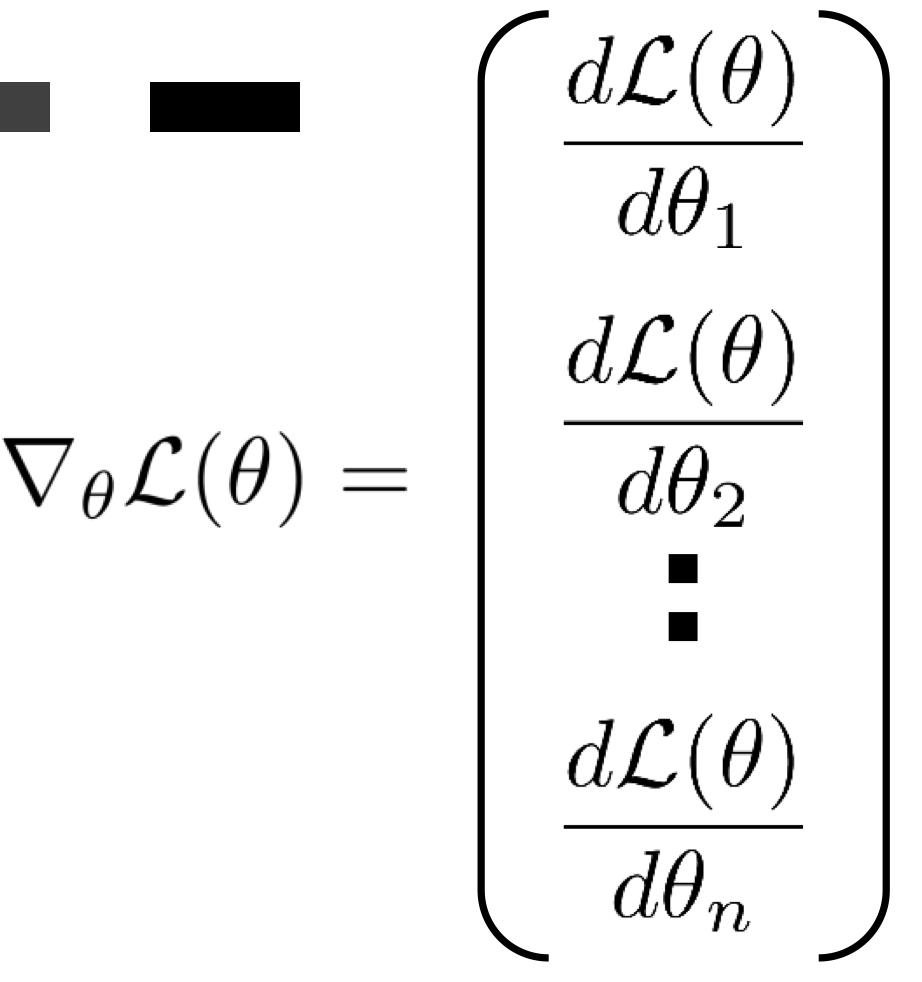
Neural net을 training 시키는 데에 있어서 필요한 요소는 바로 gradient이다.
Gradient가 있어야 우리는 parameter들을 업데이트 할 수 있게 된다.
Multiple layers를 가진 neural net의 gradient를 어떻게 구할 수 있을까?
Chain rule
가장 먼저 어떻게 neural net에서 chain rule이 이루어지게 되는지 scalar value의 변수를 통해 알아보자.
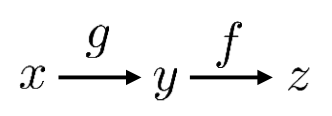
위와 같이 scalar value 변수 x, y, z가 있으며, f(g(x))의 결과가 z인 상황이다.
이때 우리는 z의 x에 대한 편미분 결과를 알고 싶다고 하면, 그것을 어떻게 구할 수 있을까?
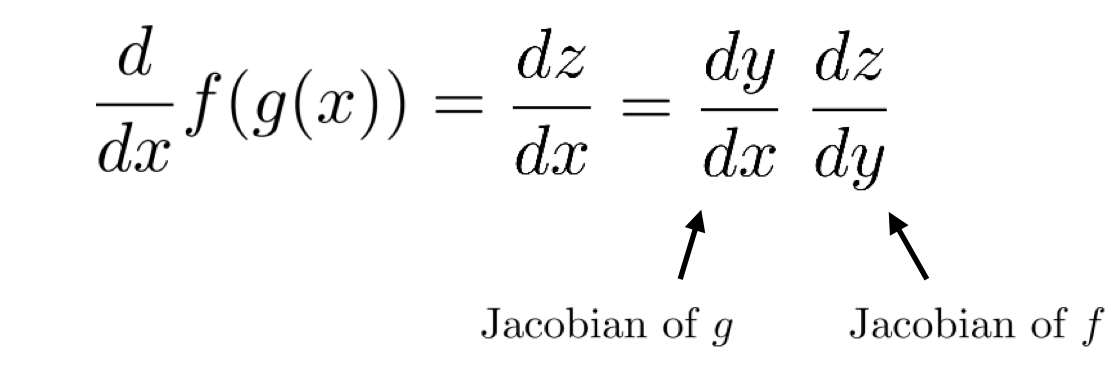
위와 같은 식으로 나타낼 수 있을 것이다.
그리고 그 값은 g의 jacobian * f의 jacobian을 진행한 결과값이다.
이제는 scalar value가 아닌 x, y, z가 아래와 같은 차원에 속해있다고 해보자.

그리고 이때 x에 대한 편미분을 진행한다고 하면, g와 f의 jacobian matrix를 통해 결과값이 결정된다.
발생하게 되는 g의 jacobian matrix의 shape은 dydx이므로 (n x m)이 되고, f의 jacobian은 dzdy이므로 (m x 1)이 된다.
위를 통해 알 수 있는 것은 2가지다.
1. 딥러닝에서는 chain rule이 일어날 때, matrix끼리의 multiplication 혹은 matrix와 vector의 multiplication이 일어난다.
2. 맨 마지막에 발생하는 jacobian은 (m x 1) 혹은 (1 x m)의 vector 형태이다.
* Jacobian matrix
Jacobian은 비선형 변환을 선형 변환으로 근사시켜주는 matrix이다.
따라서, jacobian matrix와 벡터 간의 multiplication이 진행되면 비선형 변환을 선형 변환으로 근사하는 선형 변환이 일어나는 것이다.
Chain rule for neural nets
우리는 아래와 같은 neural net에서 chain rule 식을 만들 것이다.

이를 보기 쉽게 diagram으로 표현하면 아래와 같다.
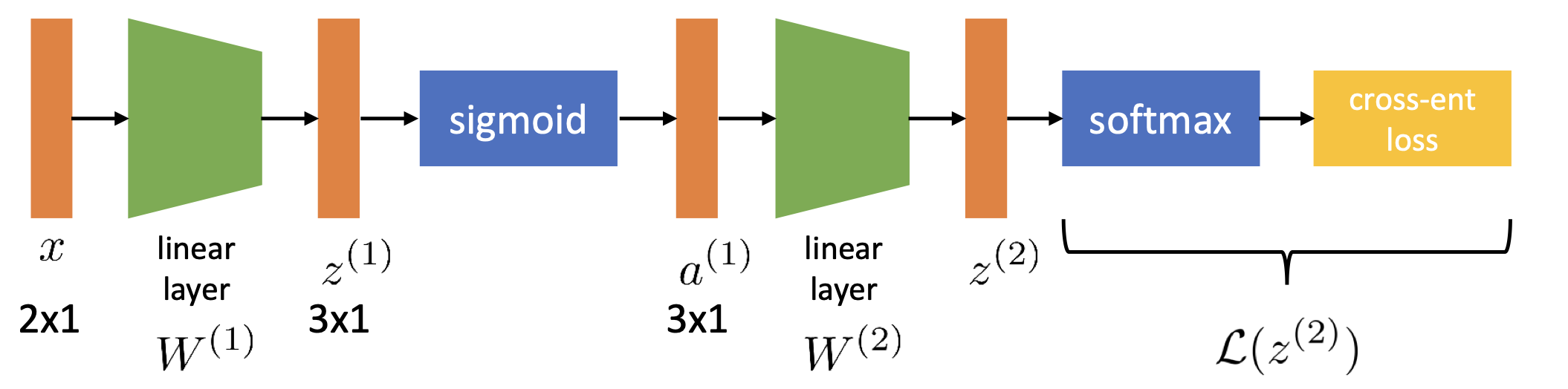
위 상황에서 우리는 parameter를 의미하는 W에 대한 편미분을 해야 한다.
그 이유는, 우리가 필요로 하는 gradient라 함은 loss function의 parameter W(θ)에 대한 편미분 값을 의미하는 것이기 때문이다.
왜 하필 parameter W(θ)에 대한 편미분이냐면, 그것이 바로 loss function들이 취하는 유일한 parameter이기 때문이다.
* L(θ)
그렇기에 우리는 loss function의 W(1),W(2)에 대한 편미분이 필요하다.
따라서 아래와 같이 chain rule 식을 작성해볼 수 있다.
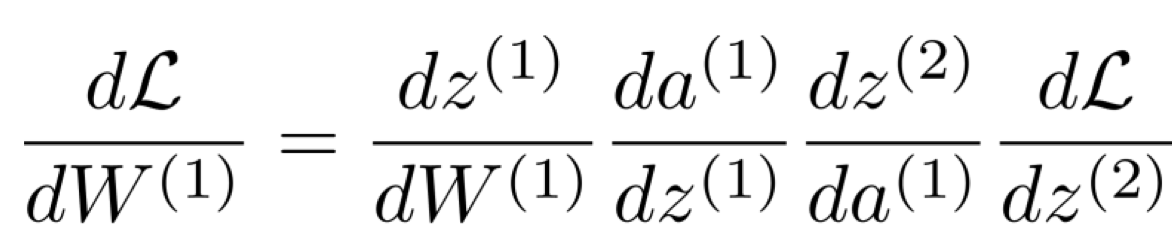
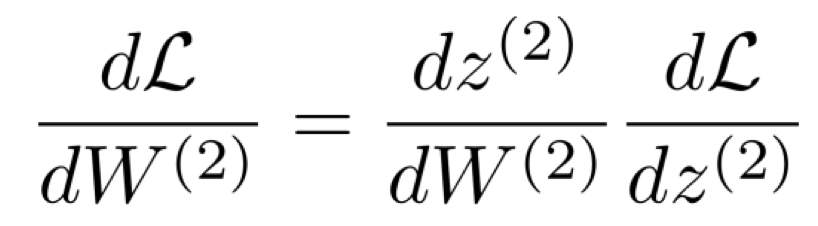
이는 아래와 같은 형태라고도 볼 수 있다.
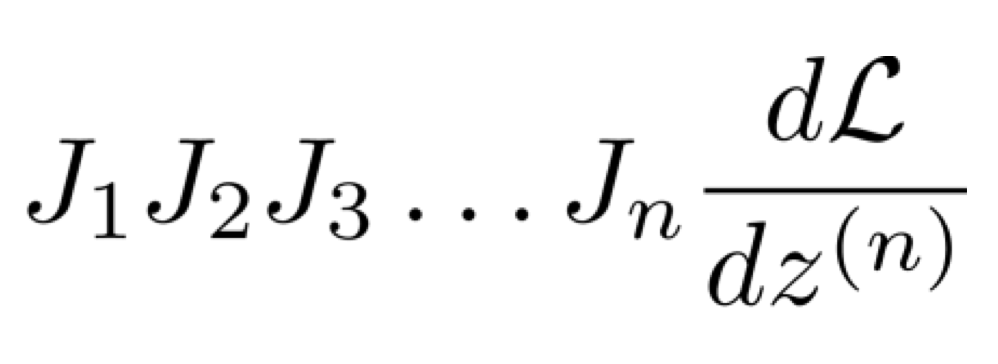
만약 위의 계산을 왼쪽부터, 그러니까 jacobian matrix끼리 multiplication을 해서 오른쪽에 도달하도록 진행한다고 해보자.
그렇다면 각 matrix multiplication을 진행하는 데에 발생하는 시간 복잡도는 O(n3)이다.
그래서 우리는 맨 마지막이 항상 vector shape으로 나타난다는 것을 이용하여 맨 오른쪽부터 gradient 값을 계산한다.
그렇게 오른쪽부터 왼쪽으로 계산을 취하면 matrix와 vector multiplication이 발생하고 이는 O(n2)이다.
Backpropagation
따라서 우리는 아래와 같이 맨 마지막의 loss function에 대한 z의 편미분을 하면 발생하는 vector를 시작으로 왼쪽으로 나아가며 matrix와 vector multiplication을 진행한다.
이것이 바로 backpropagation이다.
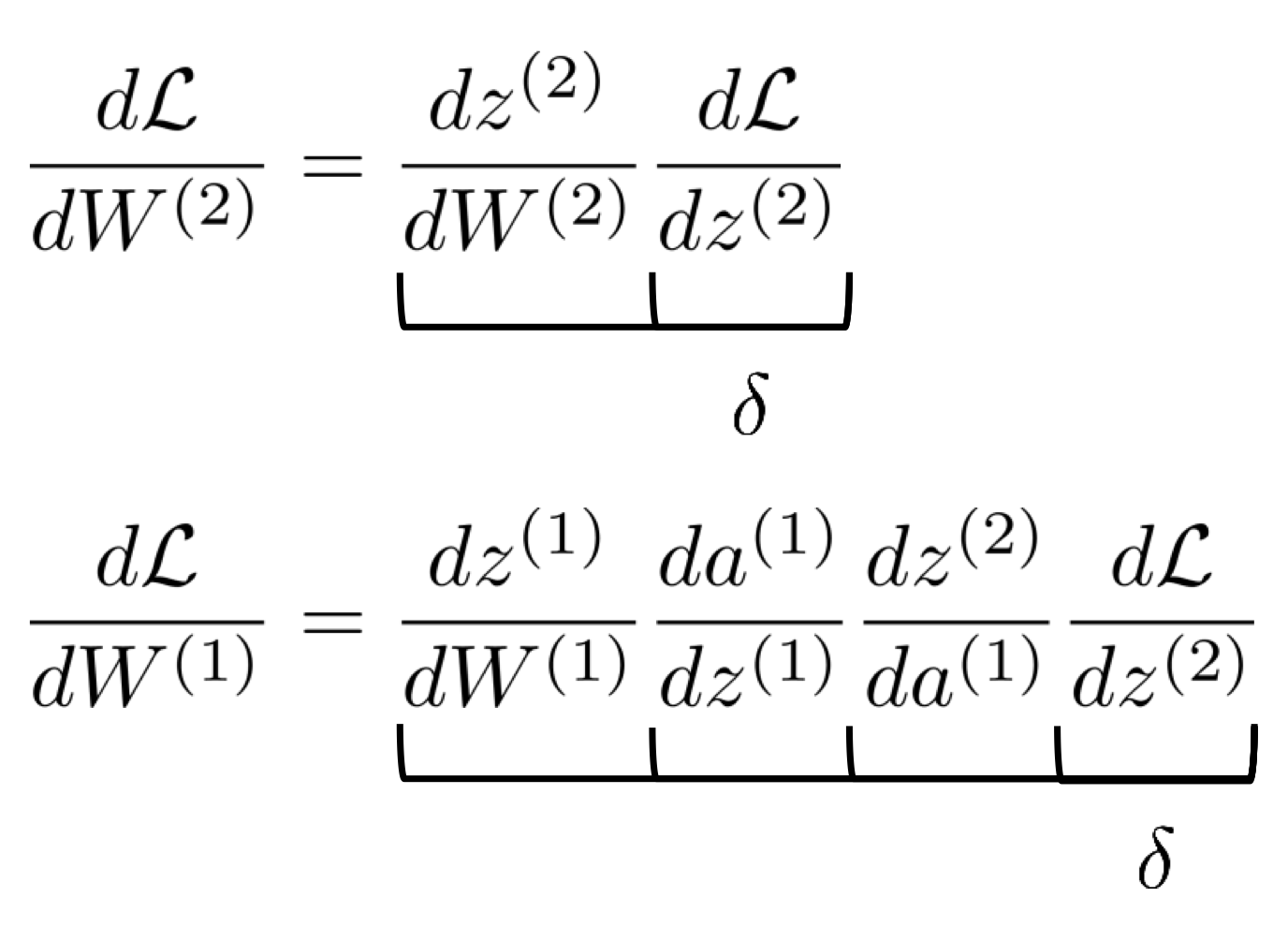
Backpropagation: linear layer
Backpropagation을 통한 기울기 계산을 위해 우리가 계산해야 하는 것은 각 function 당 2개라고 볼 수 있다.
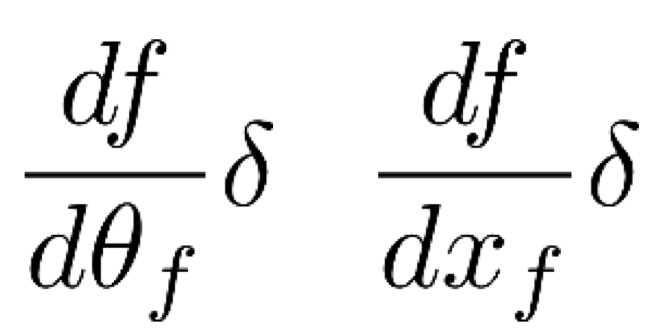
이때 θf는 weight, bias를 의미한다.
xf는 activation function의 입력으로 들어가는 x를 의미한다.
하나씩 편미분을 진행하여 backpropagation 과정을 살펴보자.
우리의 function은 아래와 같이 정의한다.
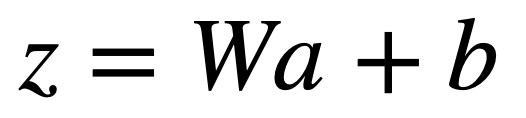
위의 z는 여러 layer에서 발생한 z를 모두 concat 해놓은 것이다.
즉, 아래 여러 layer z의 concat 버전이라는 것이다.
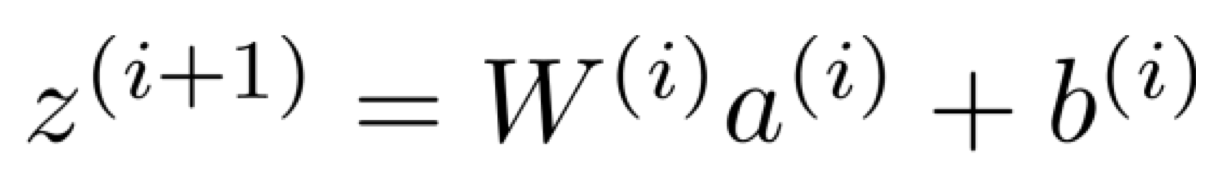
dzdWδ
dzdW은 backpropagation 중 가장 복잡하다고 볼 수 있다.
그 이유는 W가 matrix이기 때문이다.
따라서, 이를 scalar value 단위로 쪼개보자.
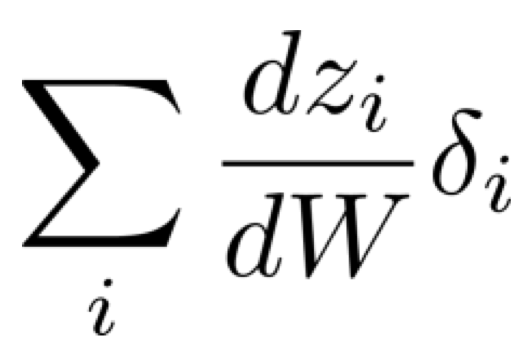
그리고 zi를 나타내보면 아래와 같다.
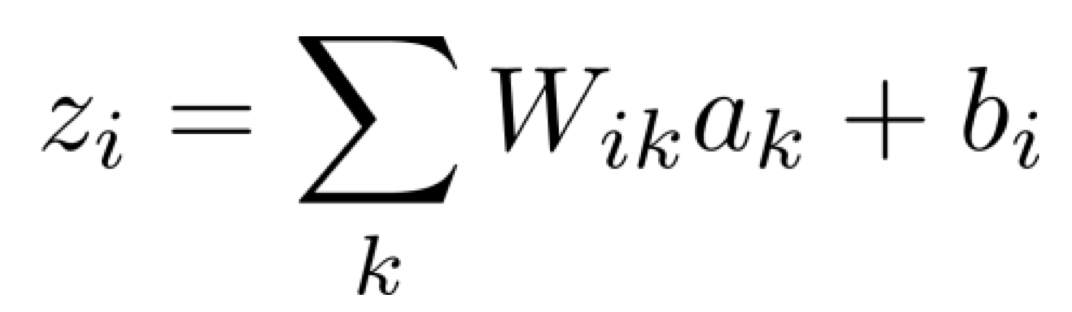
그렇다면 우리는 결국 아래를 계산하고 있는 것이다.
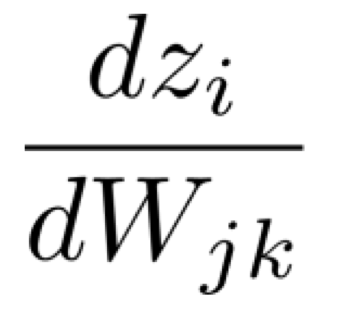
만약 현재 i가 3이라고 생각해보자. 그렇다면 우리는 3번째 layer의 z3의 W를 편미분하고자 하는 것이다.
근데 사실 3번째 layer의 z에 영향을 주는 weight W는 3번째 layer의 weight인 W3뿐이다.
즉, i와 j가 같지 않다면 그때의 W에 대한 편미분의 값은 모두 0이다.
하지만 만약 i와 j가 같다면 그때의 W에 대한 편미분 값은 ak가 된다.
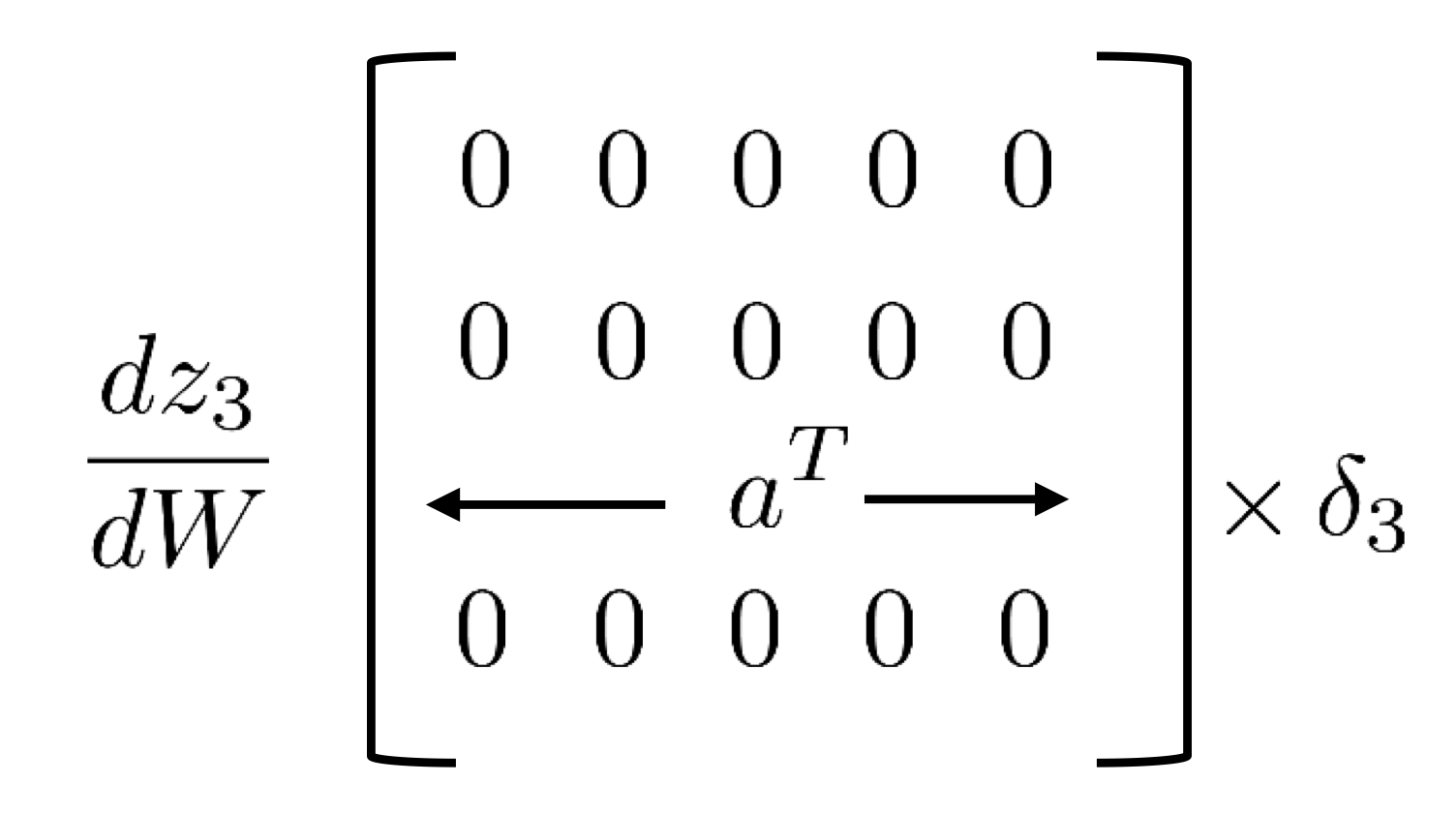
그리고 이와 같은 흐름을 모든 layer에 적용한다면 최종적으로 dzdW는 아래와 같은 모습인 것이다.
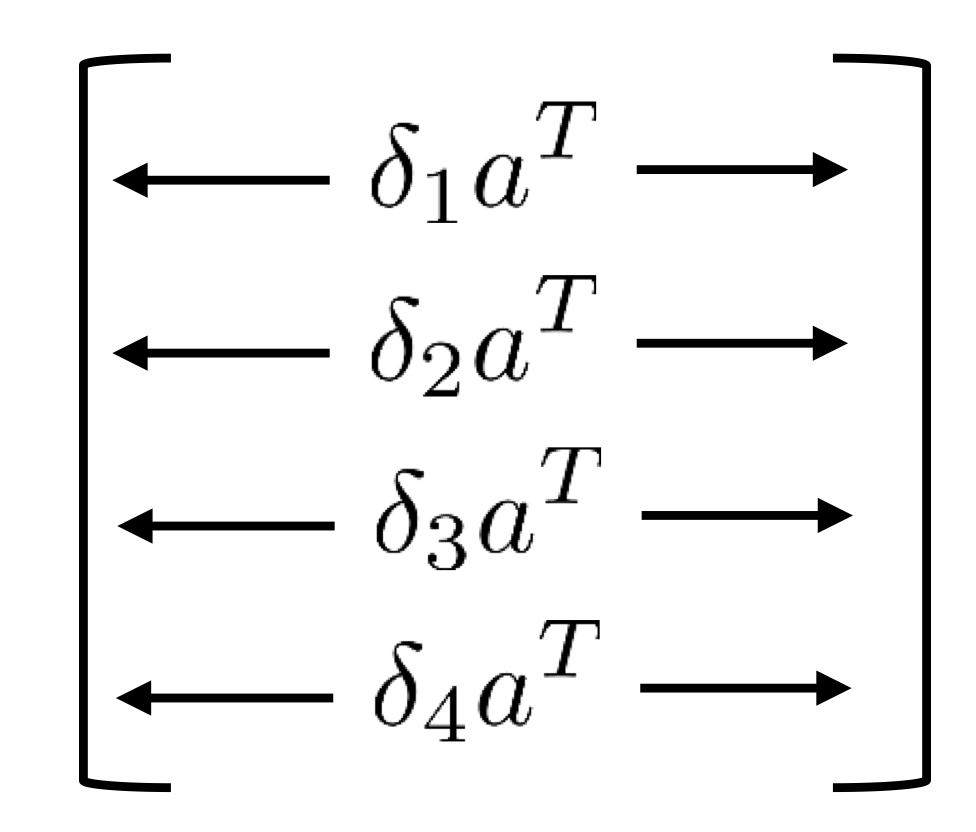
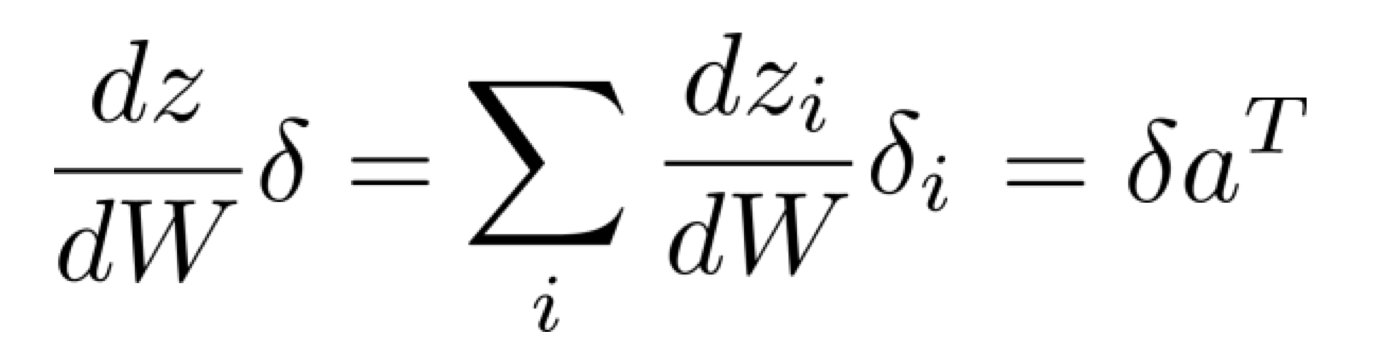
dzdbδ
위에서 했던 것과 마찬가지로 scalar value 단위로 쪼개보자.
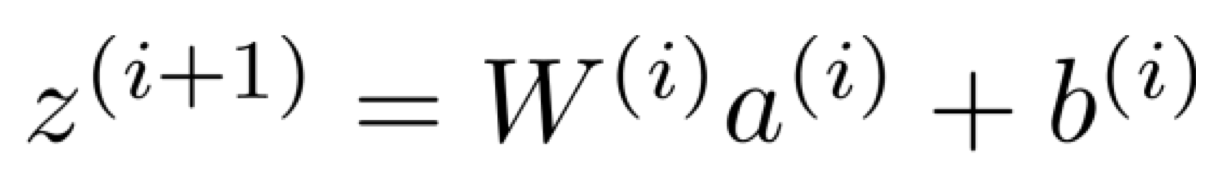
이때 우리가 하고 싶은 건 아래와 같다.
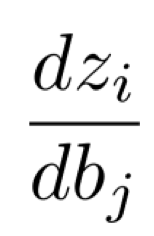
Bias에 대한 편미분 또한 weight에 대해 편미분을 할 때와 같이 i와 j의 index가 맞아야만 기울기 값이 존재하게 될 것이다.
i와 j의 index가 맞지 않는다면 그 모든 값은 0이 된다.
더불어, bias에 대해 편미분을 하면 1이라는 값이 나오게 되고 이 값들은 모든 bias에 대한 편미분 값들을 합쳐 matrix 형태로 만들게 되면
1의 값이 diagonal하게 존재하는 identity matrix가 만들어지게 된다.
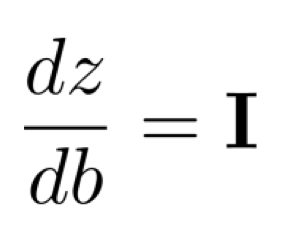
따라서, 이를 δ와 곱하게 되면 δ가 된다.
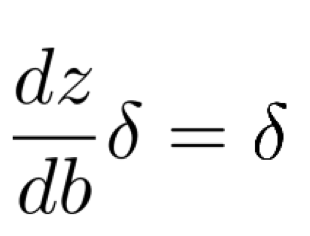
dzdaδ
위에서 했던 것과 똑같이 scalar value 단위로 쪼갠 후에 구해보면 아래와 같다.
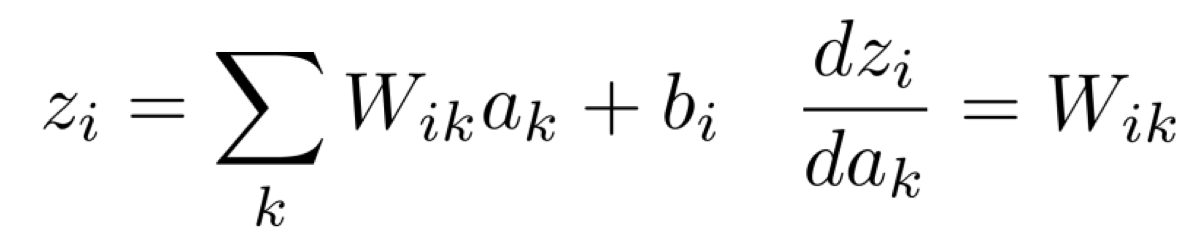
그렇다면 이때, dzda는 어떤 결과값이 나타날까?
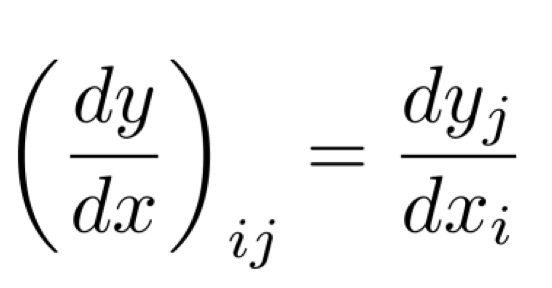
index 표기는 위와 같이 나타나므로 우리는 dzda의 결과값을 아래와 같다고 말할 수 있다.
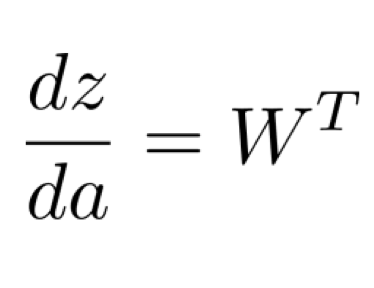
Backpropagation: sigmoid
Sigmoid의 파라미터에 대한 편미분은 일반적인 sigmoid 미분의 결과값인 (1 - σ(z))σ(z)와 같다.
그리고 sigmoid는 per-dimension 연산이기 때문에 bias에 대한 편미분을 진행했을 때와 같은 모습으로 값들이 나타난다.

References
CS 182: Deep Learning
Head uGSI Brandon Trabucco btrabucco@berkeley.edu Office Hours: Th 10:00am-12:00pm Discussion(s): Fr 1:00pm-2:00pm
cs182sp21.github.io
https://angeloyeo.github.io/2020/07/24/Jacobian.html
자코비안(Jacobian) 행렬의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
'자연어 처리 과정' 카테고리의 다른 글
| Quotient rule for derivative of softmax with respect to fk(x) (0) | 2023.08.09 |
|---|---|
| What does "linear in parameters" mean in linear regression? (0) | 2023.07.31 |
| Regularization (0) | 2023.07.26 |
| Error analysis (0) | 2023.07.26 |
| Logistic regression (0) | 2023.07.23 |


