* 이전 글과 내용이 이어집니다.
https://onebyonebyone.tistory.com/191
Error analysis
Empirical risk 우리가 모델 학습을 위해서 가설과 loss function을 정의하는 것까지 완료했다고 생각해보자. 그럼 이제 우리는 모델을 학습할 일만 남았다. 그런데 여기서 한 가지 의문이 생길 수 있다.
onebyonebyone.tistory.com
How do we regulate bias and variance?
우리는 overfitting과 underfitting 발생 원인이 variance와 bias의 tradeoff라는 것을 알게 되었다.
그럼 variance와 bias를 어떻게 잘 조절하면 overfitting과 underfitting의 문제를 해소할 수 있을 것으로 보인다.
그걸 어떻게 할 수 있을까?
* 지금부터는 overfitting 문제의 해소 방법에 대해서만 살펴볼 것이다.
12차항 function으로 polynomial regression을 하고 있다고 가정하자.
Get more data
Variance를 줄일 수 있는 좋은 방법이다. 따라서, overfitting이 해소될 것이다.
Change the model class
작은 모델로 변경한다면, variance를 줄일 수 있을 것이다.
하지만, 모델을 변경하거나 데이터를 추가로 구하지 않고도 variance를 줄여 overfitting을 해소할 수는 없을까?
Regularization
Regularization을 추가해준다면 우리는 모델 변경이나 데이터 추가 없이도 variance를 줄여 overfitting을 해소할 수 있다.
Regularization은 loss function에 추가되어 variance를 경감시켜주는 것을 말한다.
(아래에 더 정확히 묘사되겠지만, 엄밀히 말하자면 penalty term이 loss function에 추가되며, penalty term을 추가해준 것을 regularization을 추가해준 것이라고 말할 수 있다.)
The Bayesian perspective of regularization
Regularization을 유도하는 과정을 bayesian 관점에서 살펴보자.
단, 이것이 regularization을 바라보는 유일한 관점은 아니다.
High-level적으로 봤을 때, bayesian은 function이 높은 variance를 갖게 되는 것은 데이터가 수많은 solution 중 어떤 것을 취해야 하는지 결정하는 데에 있어서 불충분한 정보를 주기 때문이라고 말한다.
* 주로 variance가 높은 상황은 underdetermined 상황에서 발생한다.
(변수보다 방정식의 개수가 더 많을 때 -> 데이터셋이 너무 작거나, 모델이 너무 클 때)
즉, underdetermined 상황이라는 말은 무수히 많은 solutions가 존재하게 된다는 말과 같게 된다.
그 solutions 중에서는 variance가 높지 않은 해도 존재하겠지만, overfitting을 발생시키는 해도 존재할 것이다.
그 수많은 solutions 중 어떤 solution을 취해야 하는지 data들이 근거를 주어야 하는데, 그 정보가 불충분할 때 overfitting이 발생하게 된다고 주장한다.
그러한 생각의 흐름으로 bayesian들은 아래와 같은 의문을 갖게 된다.
Q. If there is not enough information in the data, can we give more information through the loss function?
위의 의문을 해소하기 위해 우리는 아래의 질문에 대해 생각해보자.
Q. Given D, what is the most likely$\vec{\theta}$?
우리에게 아래와 같은 data pair로 이루어진 데이터셋 D가 있다고 해보자.

이렇게 데이터셋 D가 주어졌을 때, 어떤 $\vec{\theta}$를 얻을 확률은 어떻게 나타낼 수 있을까?
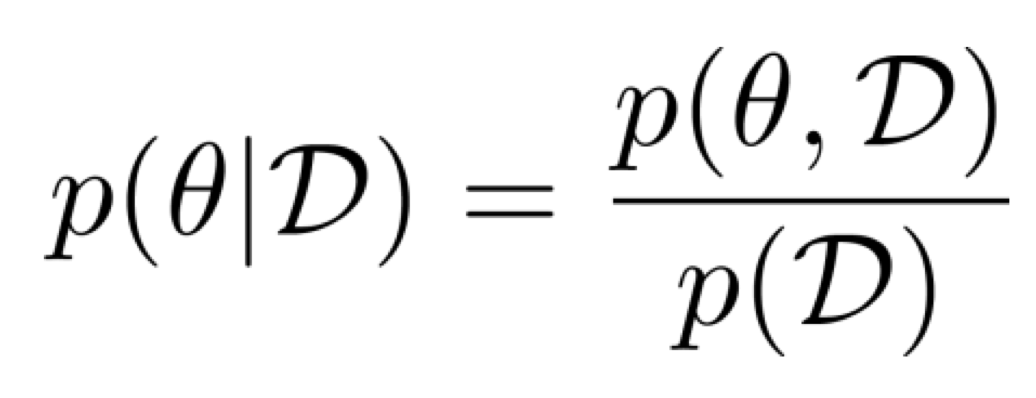
조건부확률은 위와 같이 나타낼 수 있을 것이다.
우리는 이것을 이용하여, 결합 확률로 다시 나타내보려고 한다.

Chain rule을 이용하여 조건부확률 $\theta$ given D를 둘의 결합 확률로 나타내면 위와 같이 나타낼 수 있다.
$\theta$와 D의 결합 확률은 2가지 요소로 이루어져 있다.
P(D | $\theta$)
이는 해석하면 $\theta$가 주어졌을 때, 데이터셋 D가 샘플링될 확률이다.
사실 이는 i.i.d. 가정을 따른다고 했을 때 데이터셋 D가 샘플링될 확률은 아래와 같이 나타낼 수 있었다.

Then, what is the P($\theta$)?
이는 $\theta$가 데이터셋 D를 보기 전에, $\theta$가 어떻게 형성될 것 같은지 추정하는 역할을 한다고 한다.
그리하여 이는 prior라고 불린다고 한다.
우리는 이 P($\theta$)를 loss function에 붙여서 penalty term의 역할을 하도록 한다.
P($\theta$)의 분포를 우리가 정해줌으로써, 우리는 $\theta$가 어떤 분포를 가질 것인지 미리 알려주어야 한다.

P($\theta$)가 어떤 분포를 갖도록 하는 것이 좋을까?
우리는 variance가 높은 상황인 overfitting 상황을 해소하고자 하고 있다.
overfitting일 때는, true function과는 관계 없이 무조건 data point에 fit 되는 function output이 나타나게 된다.
그리고 데이터가 변화할 때마다 그 데이터들에 민감한 반응을 보여 항상 training data에 fit을 시킬 것이다.
이러한 일들이 발생했다는 것은 large coefficient들이 존재하고 있다는 걸로 볼 수 있다.
만약 우리의 function에 large coefficient들이 존재하고 있다고 해보자.
그렇다면, 높은 차수의 항이 large coefficient를 갖고 있을 가능성도 분명 존재할 것이다.
만약, 높은 차수의 항이 large coefficient를 갖고 있다면 그 function이 그려내는 output은 데이터가 변화할 때마다 값이 급격하게 변하게 되므로 상대적으로 spiky한 function output이 나타나게 될 것이다.
즉, variance가 높게 될 가능성이 커지는 것이다.
따라서, 좋은 분포는 small numbers에 높은 probabilities를 주는 분포일 것이다.
그러한 역할을 gaussian 분포가 해줄 수 있다고 한다.
P($\theta$) ~ N(0, $\sigma^2$)
따라서, 단순히 P($\theta$)가 gaussian 분포를 따른다고 가정하면, 그리고 log를 붙여주면 우리는 아래와 같이 전개할 수 있다.

여기에서 $\theta$의 영향을 받지 않는 항들 const로 치환하면 아래와 같아진다.

위와 같은 과정으로 우리는 L2 regularizer를 유도하였다.
따라서, 우리는 최종적으로 아래와 같은 loss function w/ L2 regularization(penalty term)을 얻는다.

References
'자연어 처리 과정' 카테고리의 다른 글
| What does "linear in parameters" mean in linear regression? (0) | 2023.07.31 |
|---|---|
| Backpropagation (0) | 2023.07.31 |
| Error analysis (0) | 2023.07.26 |
| Logistic regression (0) | 2023.07.23 |
| Perceptron algorithm (0) | 2023.07.23 |


