개요
Logistic regression의 분류 가설과 parameter update rule에 대해 알아보자.
Hypothesis of logistic regression
training dataset이 아래와 같은 setting을 갖고 있다고 가정한다.

이때, logistic regression이 적용하는 가설은 아래와 같다.

위 g(z)에 해당하는 functiond은 sigmoid 혹은 logistic function이라고 불리며, 아래와 같은 그래프를 형성한다.

따라서, 아래와 같다.

Perceptron algorithm의 soft한 버전이라고 생각해볼 수 있다.
어떻게 P(y | x, $\theta$)를 최대화 할 수 있을까?

다음과 같이, label이 1일 가능성과 label이 0일 가능성이 나눠진다고 생각해보자.
이 두 식을 한 줄로 정리하면 아래와 같아진다.
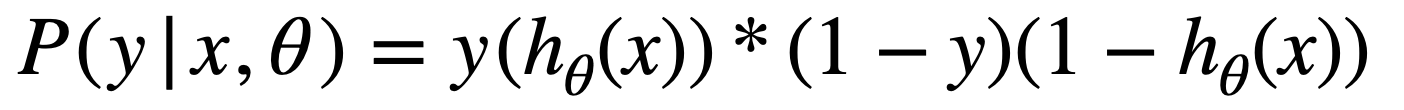
그리고 위의 확률 정의를 likelihood로 재정의해준 후, log를 붙여 log-likelihood로 만들어주자.

위의 log-likelihood에서 가설을 풀어서 보면, 그리고 summation 연산을 제거하면 아래와 같은 모습이 된다.

이제 위의 식을 사용하여 parameter $\theta$를 가지고 있을 때 label y일 log-likelihood를 계산할 수 있게 되었다.
그렇다면, 어떻게 해야 log-likelihood를 maximizing 시킬 parameter $\theta$를 구할 수 있는 것일까?
Maximizing log-likelihood with partial derivatives of l($\theta$) respect to $\theta$
The derivative of the logistic function
가장 먼저 계산의 편의를 위해 logistic function을 미분하면 어떻게 되는지부터 알아보자.

위와 같은 과정을 통해 logistic function의 미분은 g(z)(1 - g(z))임을 알 수 있다.
Parameter update rule of logistic regression
우리는 지금까지의 연산을 통해 아래의 Log-likelihood를 유도해냈다.
이제는 log-likelihood를 maximizing 시켜주는 $\theta$를 찾을 수 있도록 해주는 maximum log-likelihood 식을 유도해보자.

그렇게 하기 위해서는 우리는 $\theta$로의 편미분이 필요하다.

우리는 아래와 같은 과정을 통해 mll(maximum log-likelihood)을 얻을 수 있게 된다.


'자연어 처리 과정' 카테고리의 다른 글
| Regularization (0) | 2023.07.26 |
|---|---|
| Error analysis (0) | 2023.07.26 |
| Perceptron algorithm (0) | 2023.07.23 |
| Eigenvector, eigenvalue 그리고 diagonal과 eigendecomposition (0) | 2023.07.08 |
| Why rank(A^TA) = rank(A)? (0) | 2023.07.06 |


