개요
1. 자연어를 컴퓨터에게 이해시키기 위한 노력과 Word2vec
2. CBOW
3. Skip-gram
4. 마무리
1. 자연어를 컴퓨터에게 이해시키기 위한 노력과 Word2vec
인공지능의 분야에서 자연어 처리는 컴퓨터가 자연어를 다룰 수 있도록 하는 분야이다. 여기에서 자연어란 인간의 언어를 의미한다. 즉, 자연어 처리라는 분야는 컴퓨터가 인간의 언어를 이해할 수 있어야 하며, 그 이해를 기반으로 여러 가지 task를 해결해낼 수 있도록 한다.
그렇다면, 도대체 어떻게 컴퓨터가 인간의 언어를 이해할 수 있다는 것일까?
컴퓨터는 0과 1이라는 입력으로 많은 것을 해낸다. 결국, 자연어를 컴퓨터에게 이해시키기 위한 시작도 0과 1이 될 수밖에 없다는 것이다.
우리는 자연어를 벡터 형태로 변환하여 컴퓨터에게 자연어를 학습시키고자 한다. 엄밀히 말하면, 문장의 최소 단위는 단어이고, 단어는 의미의 최소 단위이기 때문에 단어를 벡터로 변환하여 컴퓨터에게 이해시키고자 하는 것이다.
그리고 그것을 시도하고자 사용됐던 방법들은 시소러스, 통계 기반 기법, 추론 기반 기법이 존재했다.
(1) 시소러스
유의어 사전을 말하며, 대표적인 시소러스로는 wordnet이 있다. 유의어들이 연결된 네트워크라고 보면 된다.

하지만, 이를 계속해서 사용하기에는 문제가 있었다.
자연어는 변화한다는, 유연하다는 특징이 존재하는데 그것을 실시간으로 반영할 수는 없는 방법이라는 것이다.
심지어는 새로운 단어 혹은 의미가 발생하거나, 변화하는 부분이 있다면 인간의 손이 필요하다는 부분도 문제였다.
(2) 통계 기반 기법
그러한 시소러스 기법의 문제점을 보완하고자 나온 것이 통계 기반 기법이었다. 대량의 텍스트 데이터를 의미하는 corpus를 가지고 컴퓨터에게 학습을 시켜서 컴퓨터에게 사람의 지식, 문장 구조 등의 많은 정보를 한번에 전달해주자는 방법이다.
이 방법론에서는 PPMI나 동시발생 행렬 등을 사용하여 컴퓨터에게 자연어를 이해시키고자 노력한다. 특히, 단어의 의미는 주변 단어에 의해 형성된다는 분포 가설은 통계 기반 기법의 원리가 된다.
하지만, 이러한 기법에도 문제는 존재했다. 그것은 다름아닌 데이터가 너무나도 커지게 된다는 것이었다. corpus 전체의 통계를 이용하여 단 한번에 단어들의 분산 표현(dense vector)을 얻을 수 있으나, 한번의 학습에 모든 데이터를 다 집어넣어야만 했기 때문에 연산량은 부담이 될 수밖에 없었다.
(3) 추론 기반 기법
그래서 미니배치로도 컴퓨터에 자연어를 효과적으로 학습시킬 수 있는 방법론이 등장했다.
그것은 바로 2013년 구글에서 발표한 Word2vec이다.
해당 논문에서는 컴퓨터에게 자연어를 학습시키기 위한 CBOW와 skip-gram이라는 2개의 모델을 공개했다.

이 2개의 모델을 사용하여 컴퓨터는 문장에 빈 칸을 뚫어놓아도 그 빈 칸에 어떤 단어가 들어갈지 예측할 수 있게 된다.
이를 통해 우리는 컴퓨터가 마치 언어를 이해하고 있는 것처럼 착각을 하게 된다.
* 시소러스부터 추론 기반의 기법의 시도까지 보면서 알아두어야 할 것은 컴퓨터는 학습을 통해서도 사실 단어의 의미를 알지 못한다는 것이다. 단지, 분포 가설에 따라 단어가 사용되는 맥락을 학습하여 이해하는 것이다.
위와 같은 흐름으로 컴퓨터에게 자연어를 이해시키기 위한 노력이 전개되었고 Word2vec에는 2개의 모델이 존재함을 알게 되었다. 그렇다면 이제부터는 CBOW와 skip-gram에 대해 알아보자.
2. CBOW(Continouos bag-of-words)
CBOW는 빈 칸의 주변에 있는 단어들을 입력으로 받고, 빈 칸에 어떤 단어가 들어갈지 예측하는 방법이다.

Word2vec 의 학습을 위한 CBOW 방식은 다음과 같은 메커니즘을 따른다.
예문이 "The fat cat sat on the mat"이라고 할 때, 중심 단어를 제외한 주변의 단어들이 모델의 입력으로 들어가게 되는 것이다.
이때, 몇 개의 주변 단어를 넣을 것이냐는 사용자가 정할 수 있으며 이를 윈도우 사이즈라고 한다.
CBOW를 사후 확률을 이용하여 표현하면 아래와 같다.
t-1, t+1번째 단어 즉, 주변 단어가 발생할 시 t번째 단어 즉, 중심 단어가 발생할 확률을 구하는 것이다.

학습 과정은 아래와 같다.
# 학습할 때는 1개의 hidden layer만이 존재하며, 이 layer에는 일반적인 hidden layer와는 다르게 activation function이 없기 때문에 projection layer라고 불린다고 한다. 또, 그냥 값을 projection만 해서 벡터를 만들어내기 때문에 projection layer라고 불리기도 한다.
과정 설명 전, Input layer와 projection layer 사이의 Weight의 차원 수를 VxM이라고 정의하려고 한다. V는 one-hot vector의 차원 수 즉, 단어 집합의 크기를 의미하며, M은 projection layer의 크기이다.
1. 아래와 같이 중심 단어를 sat으로 하고, 윈도우 사이즈를 2로 하여 총 4개의 주변 단어 입력이 들어간다고 하자.
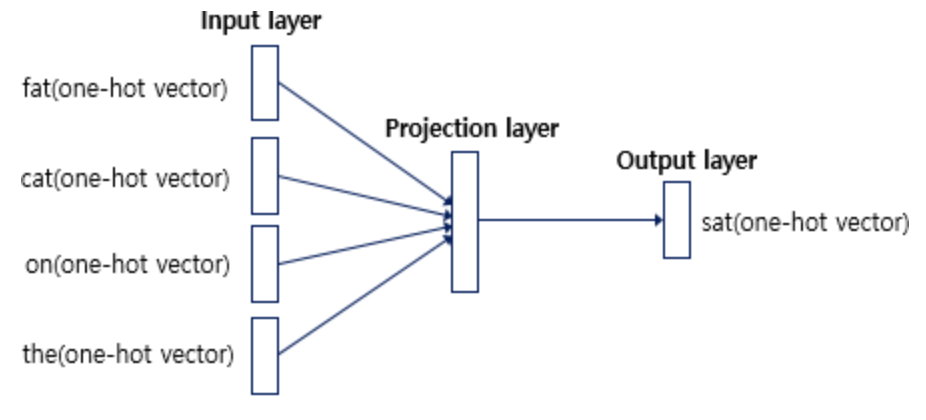
2. 그럼 4개의 단어 즉, 4개의 원핫벡터는 VxM 크기의 weight를 만나게 된다. 복잡한 신경망이라면 굉장한 연산량이 필요해질 수 있는 부분이지만, 생각해보면 현재 우리의 입력은 원핫벡터이기 때문에 별도의 계산 없이 Weight의 i번째 행을 그대로 들고 오기만 하면 된다. 그리고 weight에서 가져온 행에 들어있는 값은 사실 각 단어의 분산 표현 벡터가 된다.
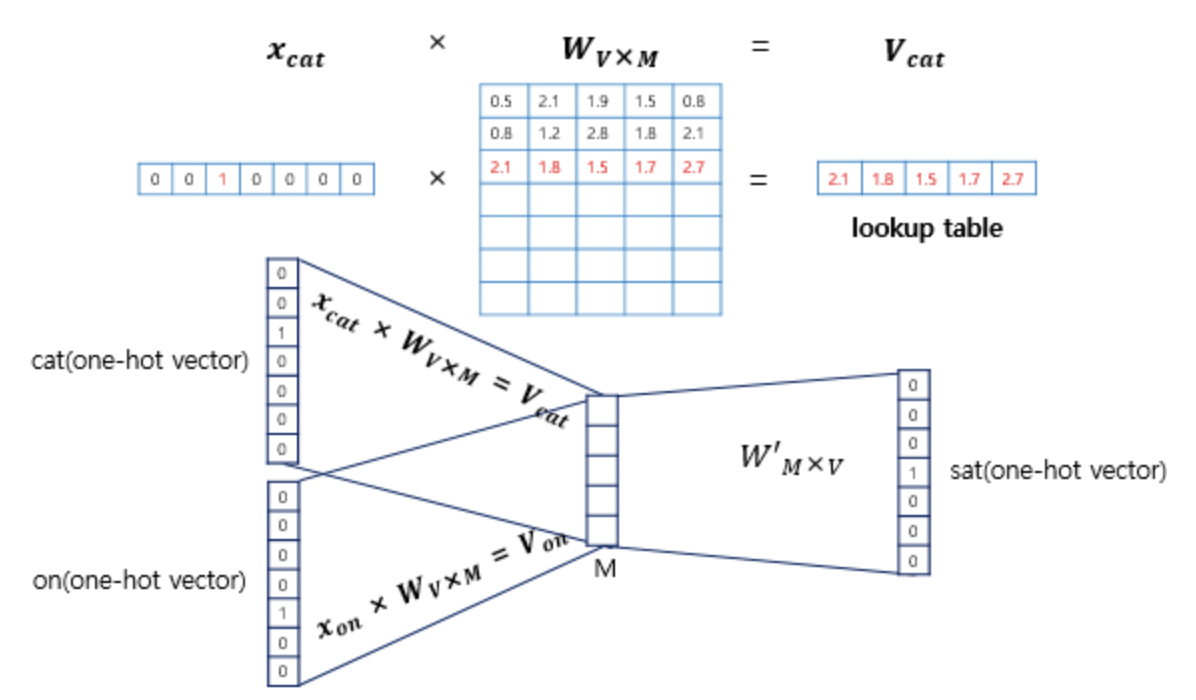
3. 우리의 입력 단어는 4개였으므로, 4개의 원핫벡터를 이용해 4개 Weight 행을 들고오면 된다. 우리는 이 4개의 입력 단어를 가지고 1개의 중심 단어를 예측하려고 하기 때문에 입력을 1개로 만들어주어야 한다. 그 방법으로 우리는 평균 벡터 1개를 만드려고 한다. 그 4개의 Weight 행을 가지고 평균 벡터 1개를 만드는 것이다. 원핫벡터를 이용해 뽑은 4개의 weight 행은 모두 더해주고 이를 나눠주는데 그 값은 윈도우 사이즈에 2를 곱해준 값이다.
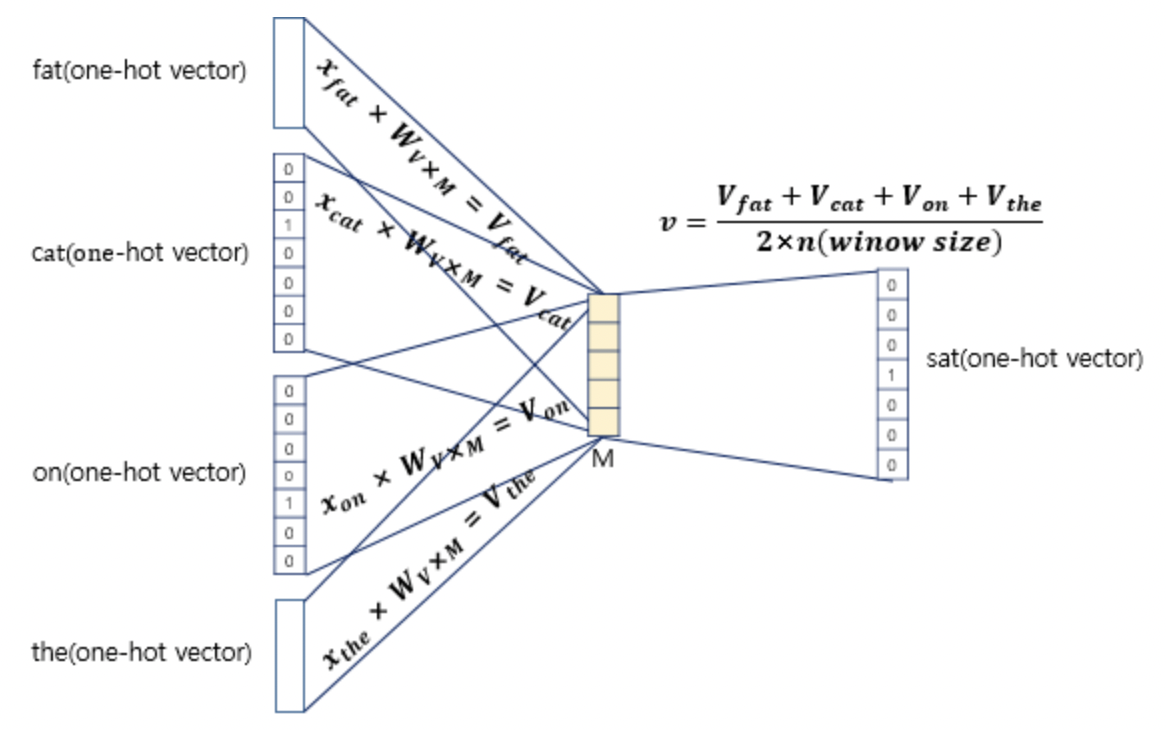
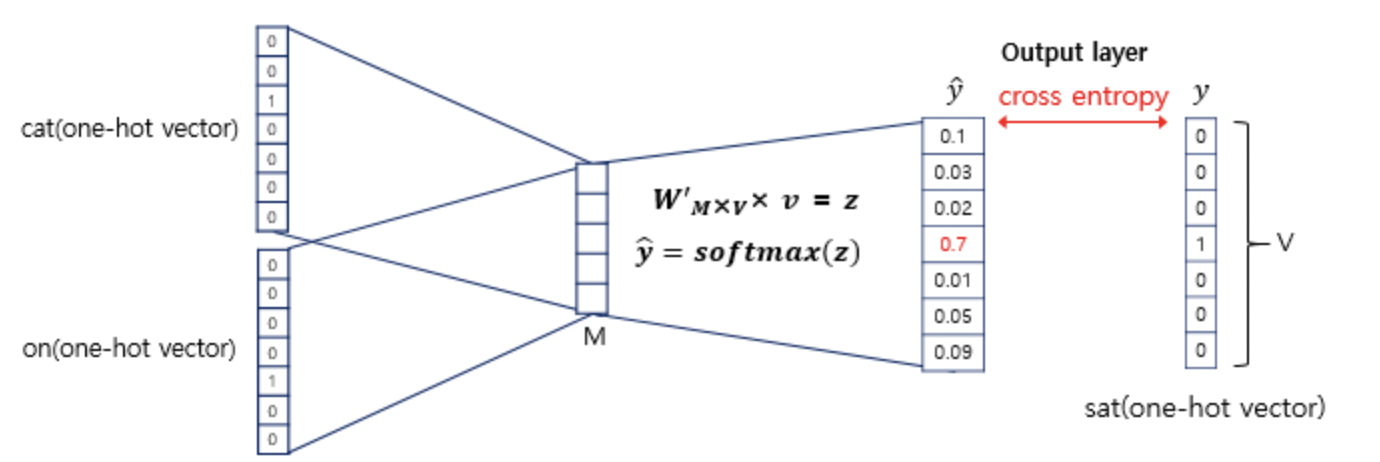
4. 그렇게 구해준 평균 벡터를 마지막 weight(MxV 사이즈)에 통과시키면 단어 집합 크기의 벡터가 하나 출력된다. 이것은 logit 벡터라고 볼 수 있으며, 이 벡터에 softmax를 취해주면 CBOW 방법을 이용한 word2vec이 어떤 단어를 중심 단어로 예측했는지 알 수 있는 것이다.
그 예측 벡터를 가지고 loss function인 cross entropy를 통과시켜주면 loss값을 얻을 수 있으며 그 loss값을 가지고 backpropagation을 하여 학습을 시킬 수 있게 되는 것이다.
3. Skip-gram
Skip-gram은 중심 단어 1개를 입력으로 받고, 주변 단어로 어떤 단어들이 들어갈지 학습하는 방법이다.
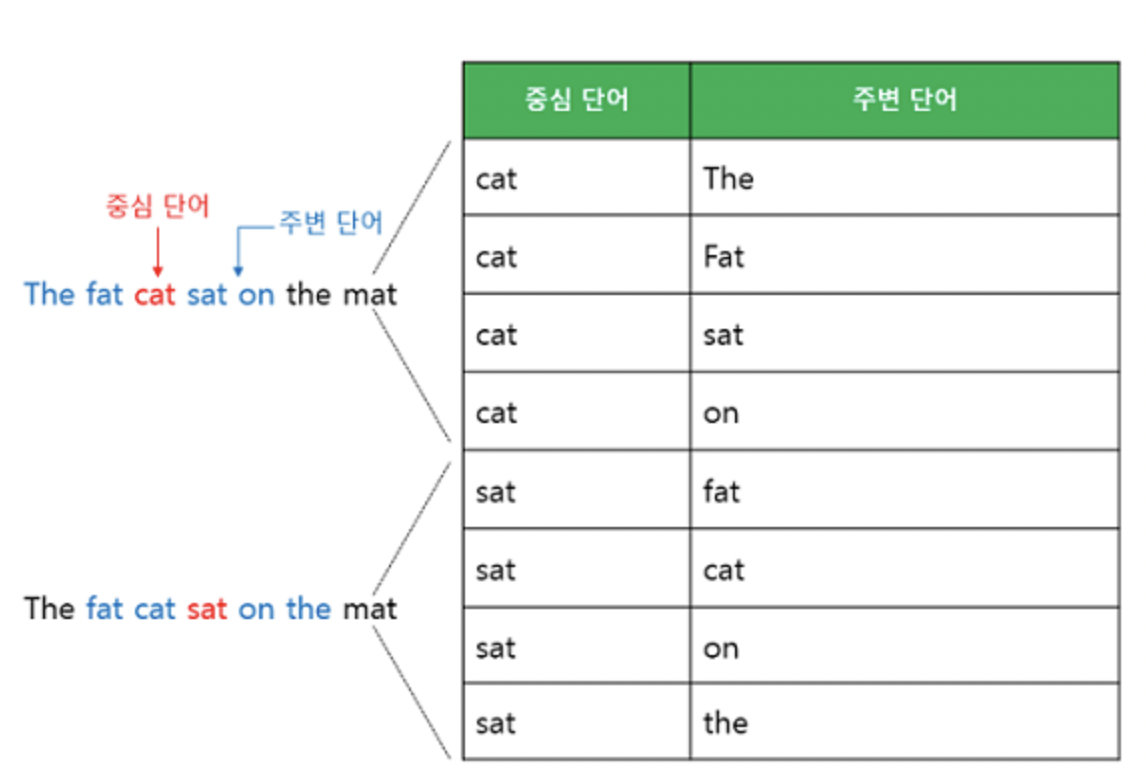
역시나 사후 확률로 skip-gram을 표현한다면 아래와 같다.
즉, t번째 단어가 발생할 시, t-1, t+1번째 단어가 동시에 발생할 확률을 구하는 것이다.
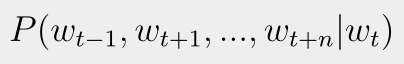
신경망은 아래와 같은 모습을 띄게 되며, CBOW와 비슷하면서도 정반대라는 특징을 갖고 있다.
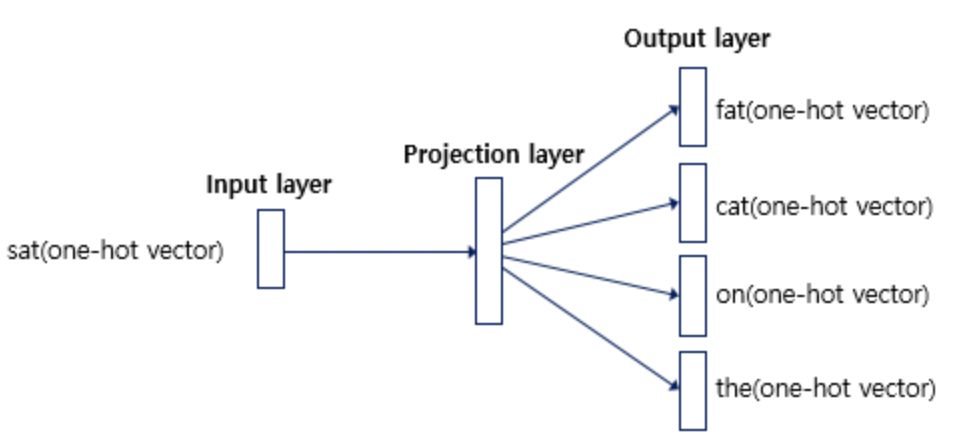
이러한 특징을 가진 skip-gram은 중심 단어 하나만 가지고도 주변 단어를 예측할 수 있게끔 하기 때문에, 윈도우 사이즈가 커지면 커질수록 결과적으로 도출되는 word vector의 quality가 좋아진다고 한다.
CBOW와 skip-gram이라는 두 방식의 성능을 비교했을 때에는 skip-gram이 더 좋은 성능을 낸다고 한다. 그 이유는 짐작컨대, 중심 단어 하나로 주변 단어를 예측해내야 하는 더 어려운 학습 방법이 채택되기 때문일 것이다.
4. 마무리
오늘은 이렇게 Word2vec까지의 역사와 CBOW, skip-gram에 대해 알아보았다. 컴퓨터에게 자연어를 사용한 task를 맡기기 위한 인간의 노력 중 초입이라고 볼 수 있을 것 같다. 이 흐름을 계속 따라가며 전반적으로 자연어 처리에 대해 이해할 수 있었으면 좋겠다.
Reference
09-02 워드투벡터(Word2Vec)
앞서 원-핫 벡터는 단어 벡터 간 유의미한 유사도를 계산할 수 없다는 단점이 있음을 언급한 적이 있습니다. 그래서 단어 벡터 간 유의미한 유사도를 반영할 수 있도록 단어의 의미를…
wikidocs.net
2. https://arxiv.org/pdf/1301.3781.pdf
위 출처에서 몇 개의 사진을 가져왔고, 내용을 참고하여 글을 작성했습니다.
'자연어 처리 과정' 카테고리의 다른 글
| Least square solution (0) | 2023.07.04 |
|---|---|
| CNN을 이용한 sequential data processing (0) | 2023.05.06 |
| Adam optimizer의 hyperparameter에 따른 학습 불가 issue (0) | 2023.05.02 |
| Sigmoid function의 forward, backward 과정 (0) | 2023.03.18 |
| 해석학적 미분과 수치 미분 (0) | 2023.03.06 |

