개요
0. Notation
1. Sigmoid function의 forward
2. Sigmoid functioin의 backward
3. Sigmoid function의 식 간소화와 의의
4. 마무리
0. Notation
글을 진행하기에 앞서, sigmoid function의 식을 다음과 같이 정의하려고 한다.

1. Sigmoid function의 forward
Sigmoid function의 forward 과정을 계산 그래프로 그려서 확인해보자.
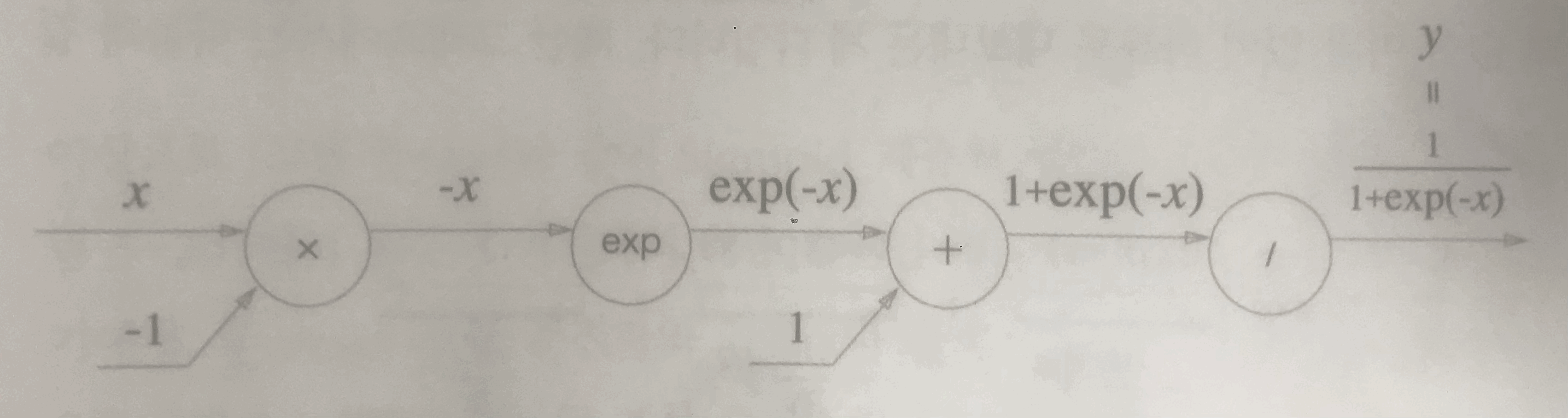
그 모습은 위의 사진과 같다.
그렇다면, 이 계산 그래프를 토대로 backward를 진행하면 어떤 연산들이 이뤄질까?
2. Sigmoid function의 backward
Sigmoid function의 backward 과정을 계산 그래프로 그려서 확인해보자.
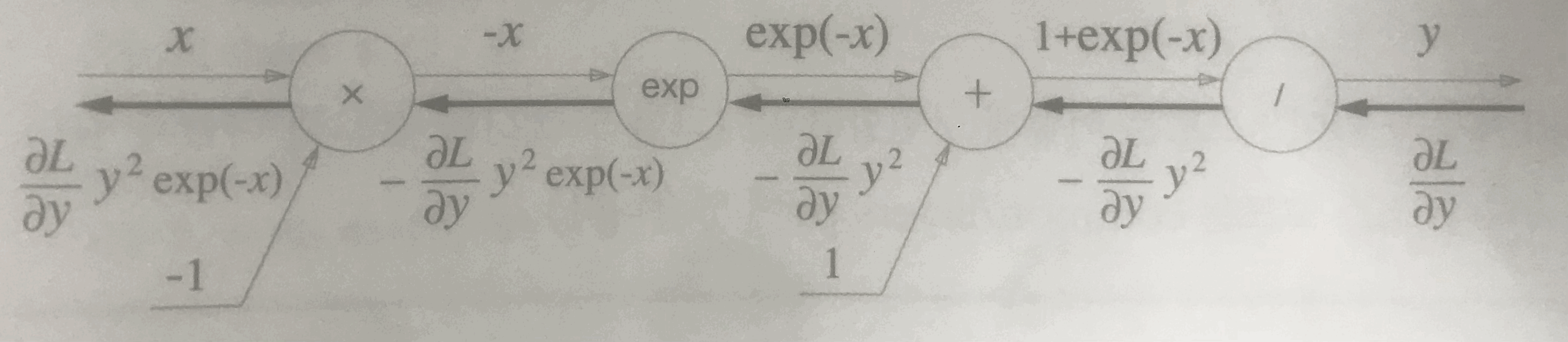
그 모습은 위의 사진과 같다.
그럼 이제 저 최종 식을 가지고 간소화를 시켜보자.
3. Sigmoid function의 식 간소화와 의의
사실 이 포스트에서 중심적으로 말하고 싶은 내용은 이번 주제에 담겨있다.
Sigmoid function의 backpropagation을 할 때 sigmoid function을 미분해야 하는데, 그때의 sigmoid function의 식이 어떻게 생겼는지 검색을 통해서 찾아보면 아래의 식을 확인할 수 있다.

한번쯤 본 적이 있는 식이라고 생각된다.
도대체 어떻게 우리가 얻은 결과인 y^2 * exp(-x)이라는 식이 위 사진과 같은 모습으로 유도될 수가 있는 걸까?
그리고 굳이 위의 모습으로 식을 간소화 시키는 이유는 무엇일까?
우선, 간소화 과정부터 알아보자.
Sigmoid function 미분 식 간소화
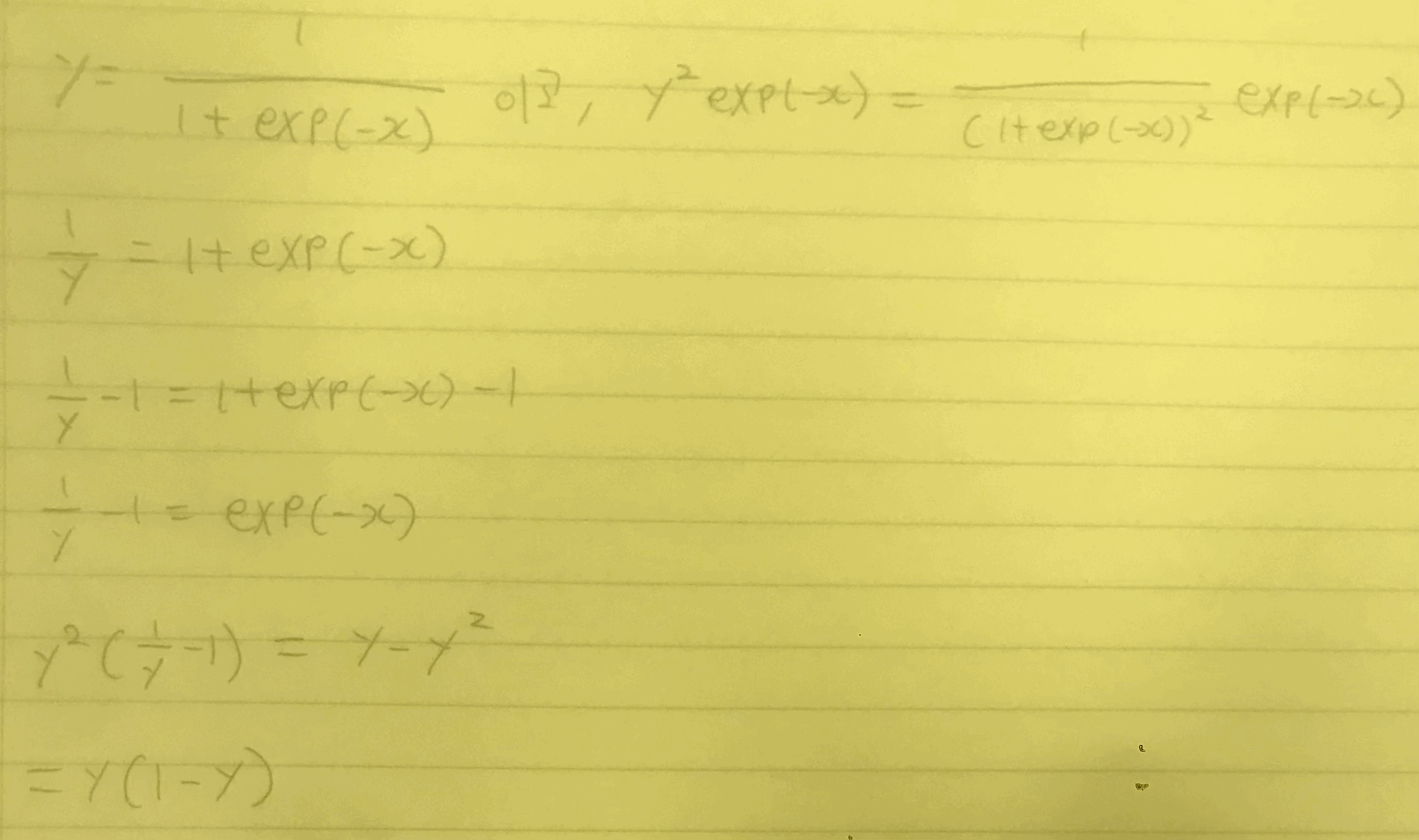
따라서 우리는 아래의 식을 얻을 수 있게 되는 것이다.

식 간소화의 의의
이렇게 식을 간소화 시키는 이유는 뭘까?
그것은 바로 중간 계산들을 거치지 않고 backpropagation 과정을 거칠 수 있다는 것에 있다.
식을 간소화 시킴으로써 무시할 수 있는 중간 계산들이란 우리가 최종적으로 유도한 식을 얻기 위해서 거쳐야 하는 모든 계산을 의미한다.
하지만 식 간소화를 함으로써 아래와 같은 과정을 무시하고 sigmoid function의 미분 결과를 얻을 수 있게 되며, 제곱 계산도 생략된다.
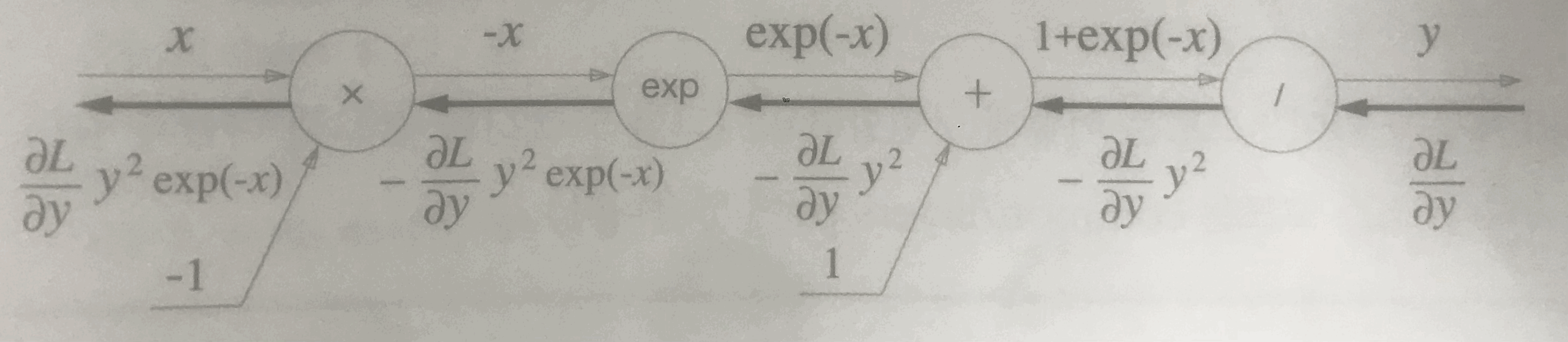
4. 마무리
오늘은 Sigmoid function의 forward, backward 연산과 미분 식 간소화에 대해 알아보았다.
라이브러리를 사용한다면 위와 같은 식을 알아야 할 필요가 있다고 딱 잘라 말할 수는 없을 것 같다. 왜냐하면, 이미 다 구현이 되어있는 걸 사용하는 데에 있어서 위의 식을 몰라도 전혀 문제가 없기 때문이다.
하지만, 직접 코드로 구현해보거나 내부적으로 일어나는 계산 과정을 이해하기 위해서는 필수적인 지식이라고 생각된다.
Reference
밑바닥부터 시작하는 딥러닝
https://www.quora.com/What-is-the-derivative-of-the-sigmoid-function
'자연어 처리 과정' 카테고리의 다른 글
| CBOW와 skip-gram (0) | 2023.05.05 |
|---|---|
| Adam optimizer의 hyperparameter에 따른 학습 불가 issue (0) | 2023.05.02 |
| 해석학적 미분과 수치 미분 (0) | 2023.03.06 |
| Training with SAM optimizer (0) | 2023.02.10 |
| Flat minima VS Sharp minima (0) | 2023.01.26 |



