개요
1. 해석학적 미분이란?
2. 수치 미분이란?
3. 전방, 후방, 중앙 차분
4. 마무리
실제로 신경망 학습의 backpropagation에서 gradient를 구하기 위해서 쓰이는 미분 방식은 아니지만, backpropagation 과정에서 미분이 사용되는 것은 명확하다. 그 이유는 gradient descent를 위해서는 기울기값을 구해야 하기 때문이다.
-> backpropagation에서 gradient를 구할 때는, 미분식을 구해놓고 거기에 x만 대입해서 기울기값을 구하는 식과 가깝다.
따라서, 미분에 대해 알아보려고 한다.
미분은 두 가지로 나누어 설명할 수 있다.
-> 해석학적 미분, 수치 미분
1. 해석학적 미분이란?

해석학적 미분은 수학에서 원하는 진정한 미분값을 구하는 것이라고 할 수 있다.
이는 함수 f에서 x에 대한 미분을 할 때의 미분값이며, 점 x에서의 접선의 기울기값이다.
즉, 목표하고자 하는 값이 x인데 그 x의 미분값/기울기값을 정확하게 구하는 것이 바로 해석학적 미분이다.
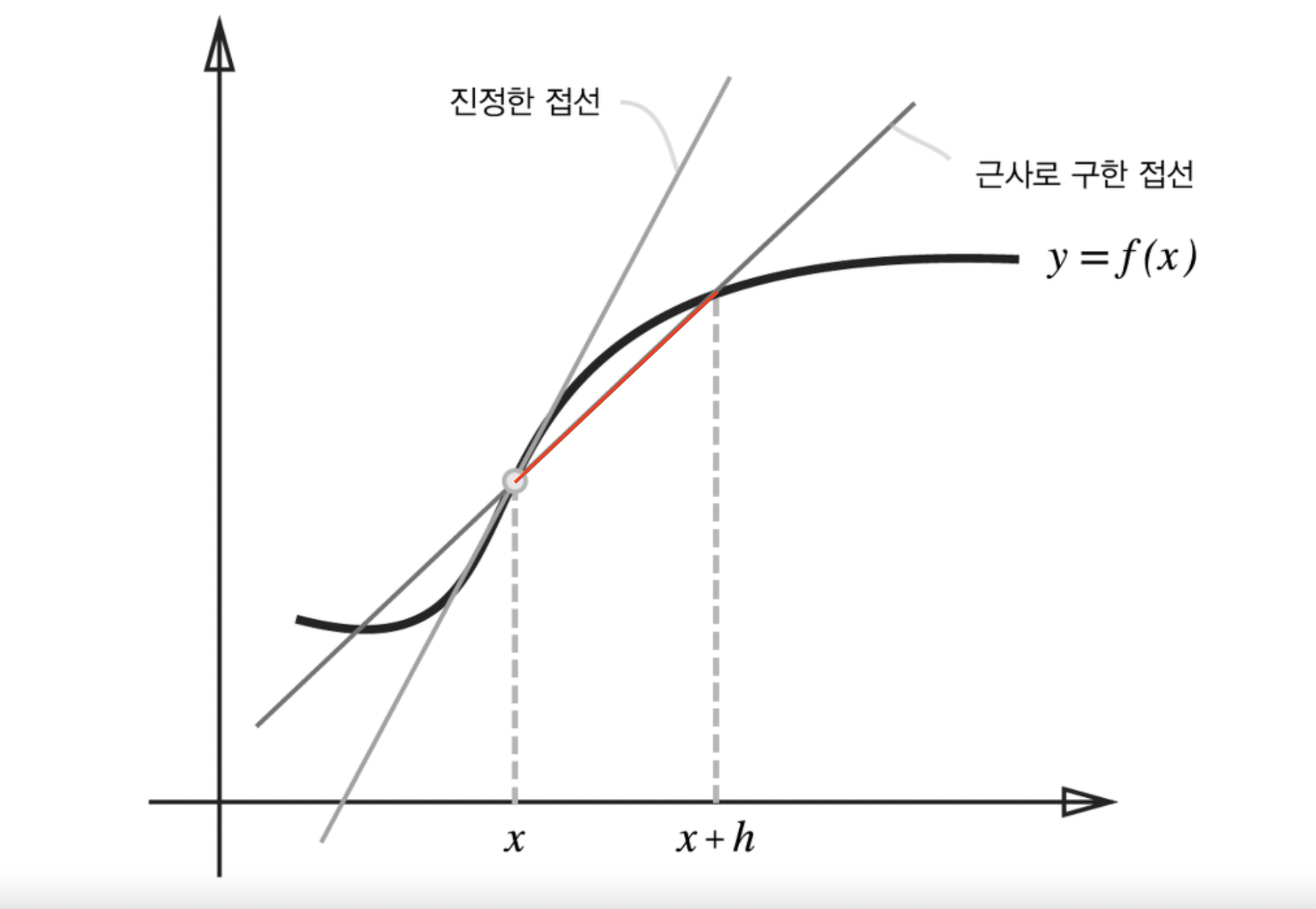
해석학적 미분에서 x의 기울기값을 구해낸다는 것은 아래 사진이 나타내는 빨간색 위치에서의 기울기값을 구한다는 말이다.

2. 수치 미분이란?

하지만, x의 함수 f에 대한 접선의 기울기값을 언제나 정확하게 구할 수는 없다.
그러나 우리는 여전히 점 x에서의 접선의 기울기값을 원하기 때문에 어떻게든 비슷하게라도 구하려고 한다.
이때, 수치 미분이 사용된다.
즉, 수치 미분은 우리가 구하고자 하는 x의 함수 f에 대한 접선의 기울기값/미분값을 근사치로 구하는 것이다.
그러면 수치 미분은 어떤 접선의 기울기를 구해서 점 x의 접선의 기울기를 근사하려는 것일까?
3. 전방, 후방, 중앙 차분
수치 미분은 x의 접선의 기울기값의 근사값을 구하기 위해 차분을 가지고 미분한다.
이때 차분이란 임의 두 점에서의 함수 값들의 차이를 말한다.
사진으로 이해하자면 아래와 같다. (사진은 전방 차분을 가지고 예를 들었다.)

즉, 우리가 목표했던 값인 정확한 x의 위치가 아닌 다른 위치에서 점을 하나 잡아 f(x)의 결과값과의 차이값을 미분한다는 것이다.
이렇게 지금까지 수치 미분의 정의와 수치 미분이 어떻게 근사값을 구하는지 알아봤다.
다시 정리하면, 수치 미분은 차분을 미분하여 근사값으 구하는데 이때 이용할 수 있는 차분으로는 총 세 가지가 존재한다.
1. 전방 차분을 가지고 근사값 구하기

식으로 나타내면 아래와 같다.
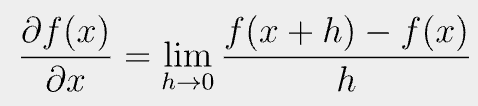
전방 차분은 x보다 전방의 위치에 점을 하나 잡아 f(x)와의 차분을 구하는 것이다.
이때, h가 의미하는 것은 x와의 차이를 말한다. h가 x에 더해지고 있으니 우리가 전방 차분에서 임의로 잡게 되는 점은 더 큰 값이 될 것이다.
이 임의로 잡은 x+h의 점에서의 함수 f에 대한 접선을 그려보면 위의 그래프 사진과 같다.
여기서 중요한 것은 기울기값을 구할 때, x+h점의 접선의 기울기를 구하는 것이 아니라 차분을 구하는 것이다.
즉, f(x)와 f(x+h) 점 사이의 접선의 기울기를 구한다는 말이다.
아래의 빨간색 위치의 기울기를 구하는 것이다.
즉, x보다 전방의 점에서 구한 접선을 가지고 차이가 나는 위치에서 기울기를 구하면 f(x)에서의 기울기값과 근사할 것이라는 생각에서 나온 것이다.
2. 후방 차분을 가지고 근사값 구하기

식으로 나타내면 아래와 같다.
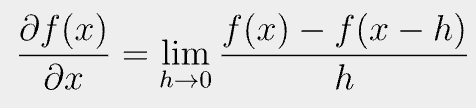
후방 차분은 x보다 후방의 위치에 점을 하나 잡아 f(x)와의 차분을 구하는 것이다.
이때, h가 의미하는 것은 전방 차분에서의 설명과 마찬가지로 f(x)의 x와의 차이를 나타내준다.
전방 차분에서와 다른 점은 x에 h만큼 마이너스가 되고 있다는 점이다. x보다 작은 값을 만들어서 f(x)의 접선의 기울기값을 근사하기 때문이다.
전방 차분과의 다른 점은 임의로 잡는 점이 x+h냐 x-h냐의 차이이지 나머지 근사 과정은 모두 같다.
후방 차분으로 f(x)의 기울기값을 근사하고자 할 때, 우리가 구해야 하는 접선의 기울기 부분은 위의 사진 기준으로 하면 아래에 초록색으로 나타난 부분과 같다.

3. 중앙 차분을 가지고 근사값 구하기
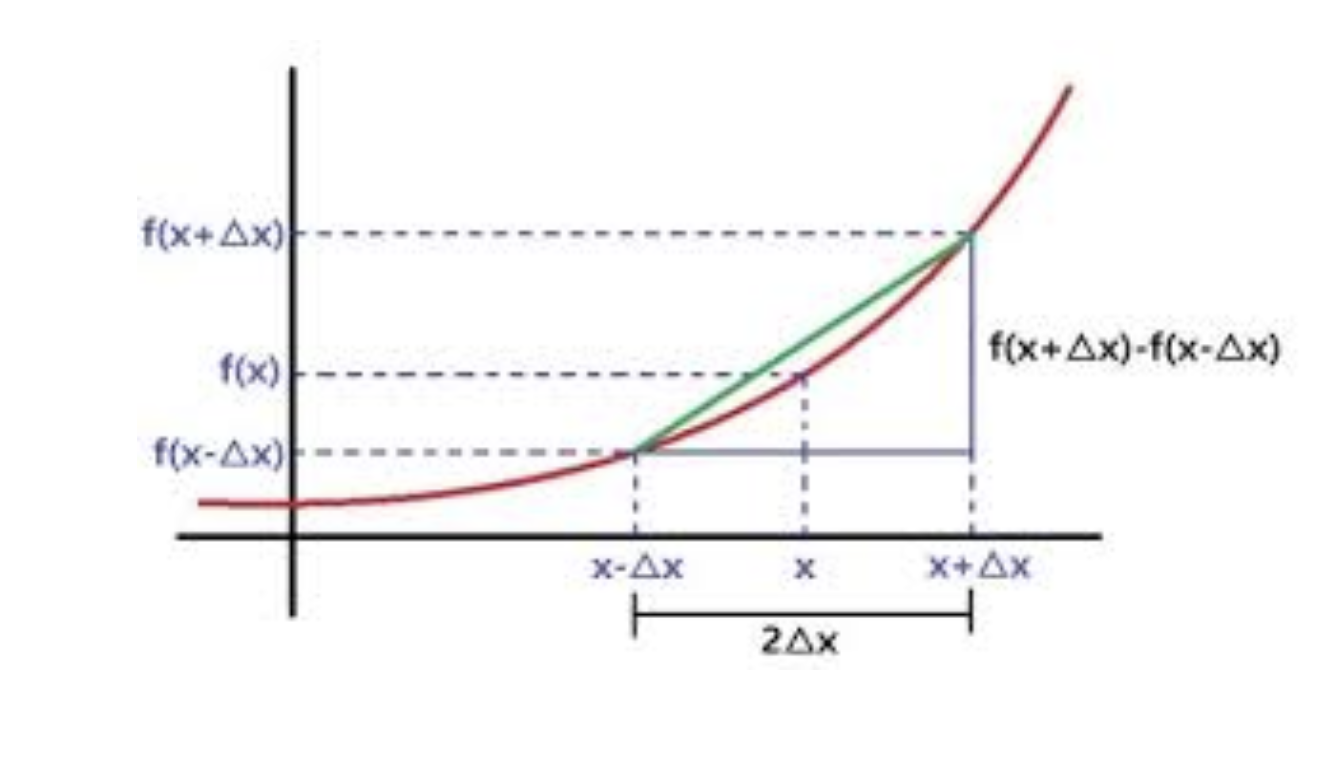
식으로 나타내면 아래와 같다.
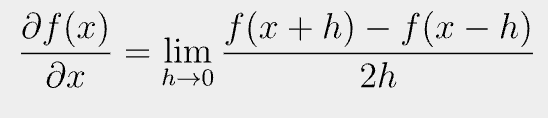
중앙 차분을 가지고 수치 미분을 하면 전방 차분과 후방 차분으로 f(x)의 접선의 기울기값을 근사하는 것보다 웬만하면 더 정확하게 값을 근사해낸다고 알려져 있다.
식을 보면, 전방 차분과 후방 차분 식에서 쓰인 x+h와 x-h가 모두 포함되어 있음을 확인할 수 있는데 실제 그래프 상으로 이해하기에도 이와 같다.
중앙 차분은 임의의 전방의 점 x+h와 후방의 점 x-h를 지나는 접선을 가지고 기울기를 구하는 방법이다.
분모에 h가 아닌 2h가 들어와있는데 이는 위 식의 유도가 전방 차분 근사식 + 후방 차분 근사식으로 이뤄져있기 때문이다.
즉, 전방 차분 근사식 + 후방 차분 근사식을 하면 중앙 차분 근사식을 구할 수 있다는 말이다.
중앙 차분 근사에서 구하는 접선은 아래의 초록색 접선이며 이것의 기울기를 구하는 것이 중앙 차분 수치 미분이다.
이 중앙 차분의 기울기를 구하는 것이 f(x)의 접선의 기울기값을 근사할 때 가장 도움이 된다고 알려져 있다.

4. 마무리
이렇게 오늘은 미분에 대해서 알아보았고, 미분의 두 가지 정의라고 할 수 있는 해석학적 미분과 수치 미분에 대해서 알아보았다.
우리는 이러한 방식으로 미분값을 구할 수 있음을 알게 되었다. 또, 정확한 미분값을 구할 수 없을 때 근사를 해서라도 미분값/기울기값을 구해낸다는 것을 배웠다.
단, 신경망 학습에서 쓰이는 backpropagation 과정에서의 미분은 이런 식의 방법으로 진행되지 않는다.
이렇게 진행이 되면 더 정확한 값을 얻을 수 있겠지만, 문제는 컴퓨터가 숫자를 표현할 때 발생하는 정밀도의 문제(반올림 오차 등)로 인해서 사용이 불가능하다.
backpropagation으로 기울기값을 구할 때에는 미분식에다가 입력값을 집어넣는 방식으로 미분값을 구해낸다는 것을 기억하자.
Reference
https://editor.codecogs.com/ 수학식 제작
'자연어 처리 과정' 카테고리의 다른 글
| Adam optimizer의 hyperparameter에 따른 학습 불가 issue (0) | 2023.05.02 |
|---|---|
| Sigmoid function의 forward, backward 과정 (0) | 2023.03.18 |
| Training with SAM optimizer (0) | 2023.02.10 |
| Flat minima VS Sharp minima (0) | 2023.01.26 |
| When an activation function is non-zero centered why it invokes zig-zag path? (0) | 2023.01.21 |



