개요
Feature scaling이란 무엇인지, 언제 쓰이는 것인지 알아보자.
Feature scaling이 필요한 이유
각 feature에는 저장되어 있는 데이터가 존재할 것이다.
예를 들어, 집값을 예측하는 모델을 만들기 위해서 데이터셋을 준비한다고 해보자.
땅의 크기, 건축년도, 방의 개수 등의 다양한 feature들이 집값 예측에 영향을 줄 것이다.
생각해보면 이 3개의 feature들은 모두 data값의 단위가 달라서 scale이 천차만별이다.
땅의 크기와 건축년도는 둘 다 천의 자리 숫자로 나오기에 그렇다고 쳐도 땅의 크기와 방의 개수를 비교해보자.
아래와 같은 데이터쌍이 존재한다고 해보자.

땅의 크기: 190m^2
방의 개수: 5개
각 데이터를 위한 단위 자체가 다르기에 값의 scale에 차이가 나고 있다.
이게 무슨 문제를 초래할까?
feature scaling을 해주지 않는다면 우리는 가중치값으로만 데이터값의 scale을 조절해주어야 한다.
그럼 땅의 크기를 x1, 방의 개수를 x2라고 할 때
땅의 크기를 위한 가중치는 10이라고 하면 1900정도의 값이 되니까
방의 개수를 위한 가중치는 약 1000정도로 설정해서 scale을 맞춰주어야 한다.
이러한 가중치를 설정하여 hypothesis를 완성시키고 그래프로 나타낸다면,

이런 모양의 그래프가 나타나게 된다.
이게 뭐가 문제냐?
x축으로는 엄청나게 급한 경사의 그래프가 나타나고 있고,
y축으로는 굉장히 완만한 경사의 그래프가 나타나고 있다.
이 그래프를 가지고 우리는 gradient descent를 해야한다.
그 결과는 아래와 같을 것이다.
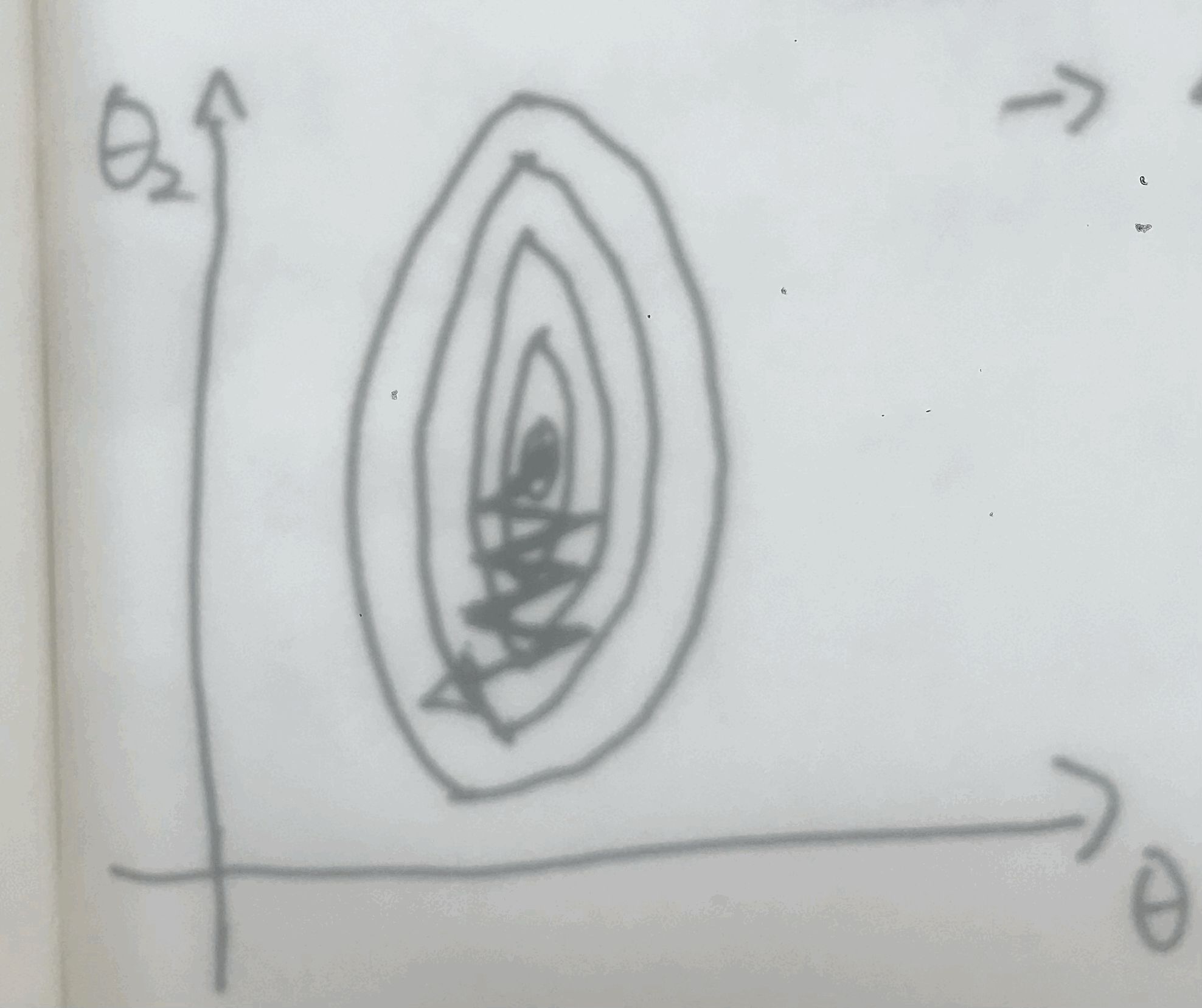
저점으로 갈 수 없는 것은 아니지만, 대각선 방향으로 이동해야 하기 때문에
저점으로 도달하기 위한 반복 횟수가 늘어나서 많은 학습 시간이 필요해진다.
왜 대각선 방향으로 이동하게 되는지?
x축 방향으로 이동하기에는 너무 기울기값이 커서 step size가 작아도 큰 보폭으로 움직이게 되어 발산할 가능성이 있고
y축 방향으로 이동하기에는 너무 기울기값이 작아서 step size가 작지 않아도 움직임이 거의 없을 수 있기 때문에
대안으로 대각선 방향으로 이동하게 되는 것이다!
이러한 상황을 피하기 위해 필요한 과정이 바로 feature scaling이다.
Feature scaling의 적용 방법
1. Max scaling
간단하다.
해당 feature에서 존재하는 데이터 중 가장 큰 값으로 나머지 데이터들을 나누어 주는 것이다.
그럼 모든 데이터값이 0 <= X <= 1의 범위로 설정된다.
2. Min-max scaling
(i) 데이터값의 범위를 0 <= X <= 1로 설정하기
해당 feature에서 존재하는 데이터 중 최솟값으로 모든 데이터값을 빼준다. 이때 최솟값 자기 자신도 포함하여 최솟값은 0이 된다.
최솟값만큼 뺀 최댓값으로 나머지 데이터들을 나누어 준다.
그럼 모든 데이터값이 0 <= X <= 1의 범위로 설정된다.
(ii) 데이터값의 범위를 -1 <= X <= 1로 설정하기
해당 feature에서 존재하는 데이터 중 최댓값과 최솟값의 중간값을 구한다.
중간값 = (최댓값 + 최솟값) / 2
이렇게 구한 중간값으로 모든 데이터값을 빼준다.
중간값만큼 뺀 최댓값으로 나머지 데이터들을 나누어 준다.
그럼 모든 데이터값이 -1 <= X <= 1의 범위로 설정된다.
3. Z-score normalization
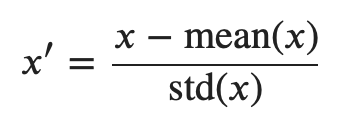
평균은 0, 분산은 1로 normalization을 하는 방법이다.
해당 feature의 모든 데이터에 대해 위의 식에 값을 대입하면 된다.
x prime이 normalization 된 값이고, x는 normalization 되기 전 값이다.
std => 표준편자
mean => 평균
'자연어 처리 과정' 카테고리의 다른 글
| Softmax function and cross-entropy loss (0) | 2022.11.30 |
|---|---|
| Cost function for Logistic regression (1) | 2022.11.30 |
| 경사하강법 (0) | 2022.11.28 |
| determinant가 0이라는 것의 의미는? (0) | 2022.11.25 |
| SVD의 이해 (0) | 2022.11.24 |



