Empirical risk
우리가 모델 학습을 위해서 가설과 loss function을 정의하는 것까지 완료했다고 생각해보자.
그럼 이제 우리는 모델을 학습할 일만 남았다.
그런데 여기서 한 가지 의문이 생길 수 있다.
Q. 우리 모델이 data를 잘 학습하고 있다는 걸 어떻게 확인할 수 있을까?
이러한 의문을 해소하기 위해서 고안된 것이 empirical risk이다.
우선 risk란, 우리 모델의 예측이 틀릴 확률을 말한다. 따라서 empirical risk는 우리가 가지고 있는 train dataset에 대해 우리 모델의 예측이 틀릴 가능성을 나타내준다. train loss라고 간주해도 무방할 것 같다고 생각한다.
그럼 도대체 이 empirical risk는 어떻게 구할 수 있는 것일까?
Risk 정의
먼저 risk에 대해 정의해보자.
우리가 아래와 같은 loss function을 정의했다고 가정하자.

그리고 데이터와 label은 아래의 데이터 실분포에서 sampling 한 것이라고 가정하자.
x ~ P(x), y ~ P(y | x)
그렇다면, 우리가 얻을 수 있는 risk의 기대값은 아래와 같다.

이렇게 risk를 정의했다.
하지만 이는 우리가 학습할 때 얻을 수 있는 risk라고 보기는 어렵다.
우리는 데이터의 실분포를 알아서 어떤 P(x)에서 데이터를 sampling 하여 사용하는 것이 아니라, 주어진 데이터셋 D에서 데이터를 가져다가 사용하는 것이기 때문이다.
즉, 우리는 아래와 같이 하지 않는다는 것이다.

Empirical risk 정의
따라서 우리는 학습을 위해 주어지는 데이터셋 D를 가지고 다시 risk를 정의한다.
이때는 empirical risk라고 칭한다.
그렇다면 우리는 주어진 D를 가지고 empirical risk를 아래와 같이 정의할 수 있다.

단지 주어진 x와 $\theta$를 이용하여 예측을 만든 후 우리가 사전에 loss function을 zero-one loss로 정의했기 때문에, label y와 다른 예측이 몇 개 존재했는지 세는 식의 empirical risk가 정의된다.
그리고 결과적으로는 empirical risk는 우리가 가지고 있는 데이터셋 D의 평균 loss가 나타내게 된다.
이렇게 empirical risk를 정의했다.
우리가 empirical risk를 정의하는 이유는 학습이 잘 이루어지고 있는지 판단하기 위해서 정의하기도 하지만, true risk를 예측, 근사하기 위해서 정의한다.
True risk는 우리가 학습 중에 만나지 않은 unseen data를 상대로 했을 때 틀릴 확률이라고 생각하면 된다. 즉, test loss라고 봐도 무방하다고 생각한다.
정의한 empricial risk를 통해, 우리는 우리의 학습이 잘 이루어지고 있는지 판단할 수 있다.
다만, 우리의 optimization은 empirical risk를 낮추는 것이 목적이며, empricial risk $\neq$ true risk이라는 것을 잘 알고 있어야 한다.
Emprical risk $\neq$ true risk이므로 발생하는 문제
위에서 언급했듯이, 우리는 학습할 때 empirical risk를 최소화하는 목적을 가지고 학습을 진행한다.
하지만, empricial risk $\neq$ true risk이기 때문에 발생하는 2가지 문제가 있다.
1) overfitting
Empirical risk는 낮지만, true risk는 높을 때 발생하는 문제다.
* dataset이 작아서 data의 개수보다 모델의 parameter 개수가 더 많을 때 발생할 수 있다.
2) underfitting
empirical risk와 true risk가 모두 높을 때 발생하는 문제다.
* model의 크기가 너무 작거나, optimizer 설정(lr, etc...)이 잘 안 되었을 때 발생할 수 있다.
이렇게 empirical risk $\neq$ true risk일 때 발생하는 2가지 문제를 high-level로 알아보았다.
Low-level 관점으로 바라본 overfitting, underfitting
overfitting과 underfitting 문제에 더 파고들어 살펴보고자 한다.
그렇게 하기 위해서 우선 regression 모델을 다룬다고 가정하겠다.
그럼 우리는 regression 모델을 위한 loss function을 정의해야 한다.
우리는 regression 모델을 통해서 아래의 확률을 최대화 하고자 한다.

그러나 우리는 y가 어떤 분포를 따르고 있는지 모르기 때문에, y가 gaussian 분포를 따른다고 가정한다.
그리고 어떤 평균과 분산을 따르고 있는지도 모르기 때문에, 우리가 가지고 있는 x와 $\theta$를 이용해 아래와 같이 가정한다.

그렇다면 우리는, 평균 $f_\theta(x)$, 분산 $\Sigma_\theta(x)$인 gaussian 분포로 y의 분포를 가정한 상황이므로 $log\ p_\theta(y | x)$는 아래와 같다.
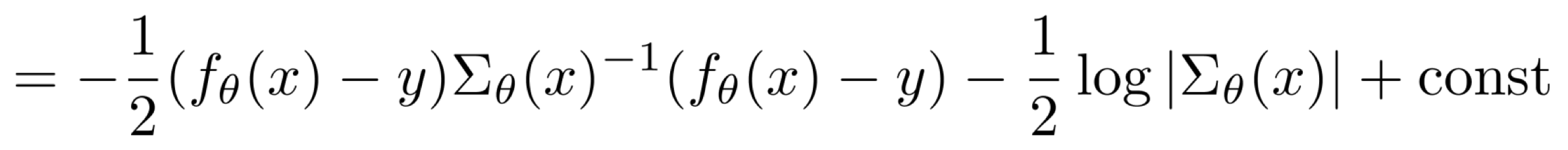
const는 $log\ 2\pi$인데, 이는 현재 어떤 parameter와도 연관이 없기 때문에 const라고 정의할 수 있을 것이다.
이때, $\Sigma_\theta(x)$를 identity matrix라고 가정해보자.
그러면 아래와 같이 위의 식이 정리된다.
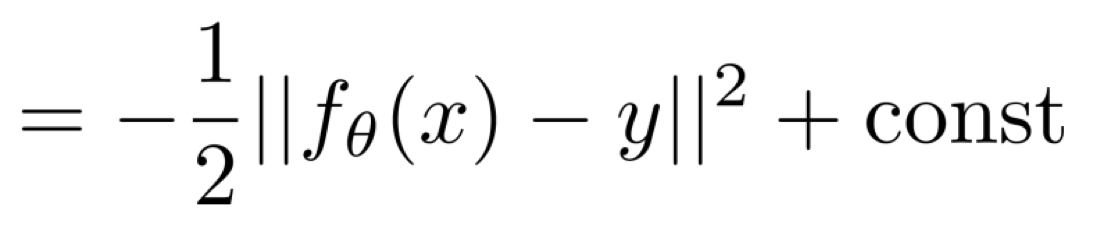
const를 제거하면, 결과적으로는 MSE loss를 얻게 되었다.
따라서, 이와 같은 과정으로 loss function을 유도해냈고, y의 분포일 확률을 maximizing하는 것은 MSE loss를 minimizing 하는 것과 같다는 것을 알 수 있다.
이렇게 regression을 위한 loss function을 얻었으니, 이제 다시 overfitting과 underfitting에 관해 이야기해보자.
좀 더 명확하게, polynomial regression 모델을 사용하는 상황이라고 가정하자.
아래는 overfitting과 underfitting의 깊숙한 이해를 유도하기 위한 질문이다.
Q. How does the error change for different training sets?
먼저 overfitting이 일어나는 상황이라고 가정하고 위의 질문에 대한 답변을 찾아보자.
When we are in overfitting
overfitting 상황에 대한 정의는 위에서 언급되었다.
empirical risk는 낮고, true risk는 높은 상황이다.
그렇다면 위의 질문에 대하여 아래와 같은 과정을 통해 답을 찾아볼 수 있다.
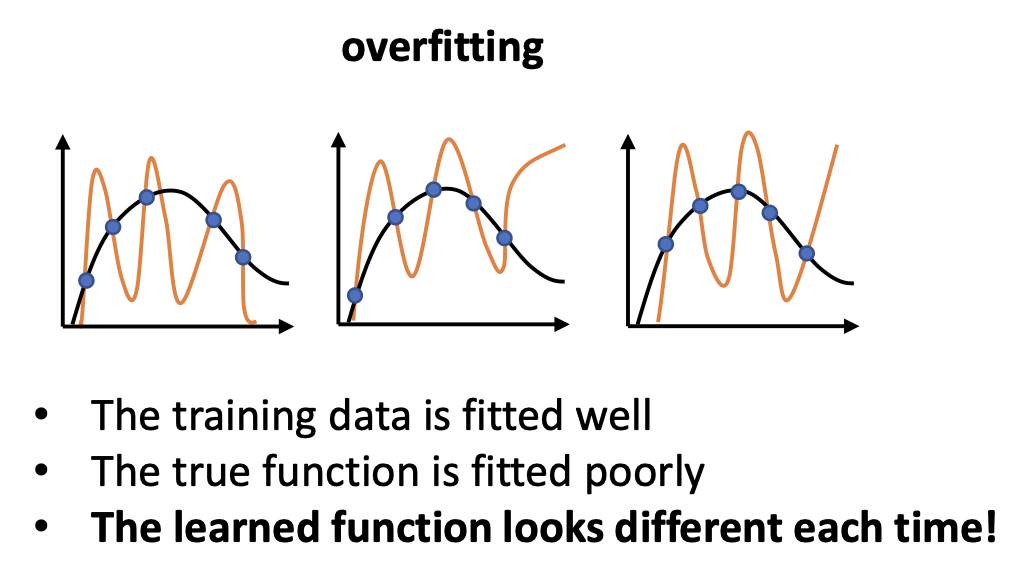
결국, overfitting인 상황이라고 가정한다면, 우리의 function이 overfitting의 결과를 낸다고 가정한다면
training set이 바뀔 때마다 function은 변하게 될 것이다.
단순하게 그 이유를 말하자면, 우리의 function은 overfitting 하고 있고, 그렇다는 말은 training data에 굉장히 잘 fit 시킨다는 뜻이다.
하지만, true function과는 거리가 멀 것이다.
즉, true function과는 상관 없이, 어떻게든 training data에 우리의 function이 fit될 것이기 때문에
다른 데이터가 들어오면 overfitting인 상황일 때는 우리의 function output이 변하게 된다.
When we are in underfitting
underfitting은 empirical risk와 true risk가 동시에 높은 상황이라고 언급하였다.
즉, 주어진 training data에도 fit 시키지 못하고, true function에도 fit 되지 못한다.
따라서 위에서 주어진 질문에 아래와 같이 답할 수 있다.
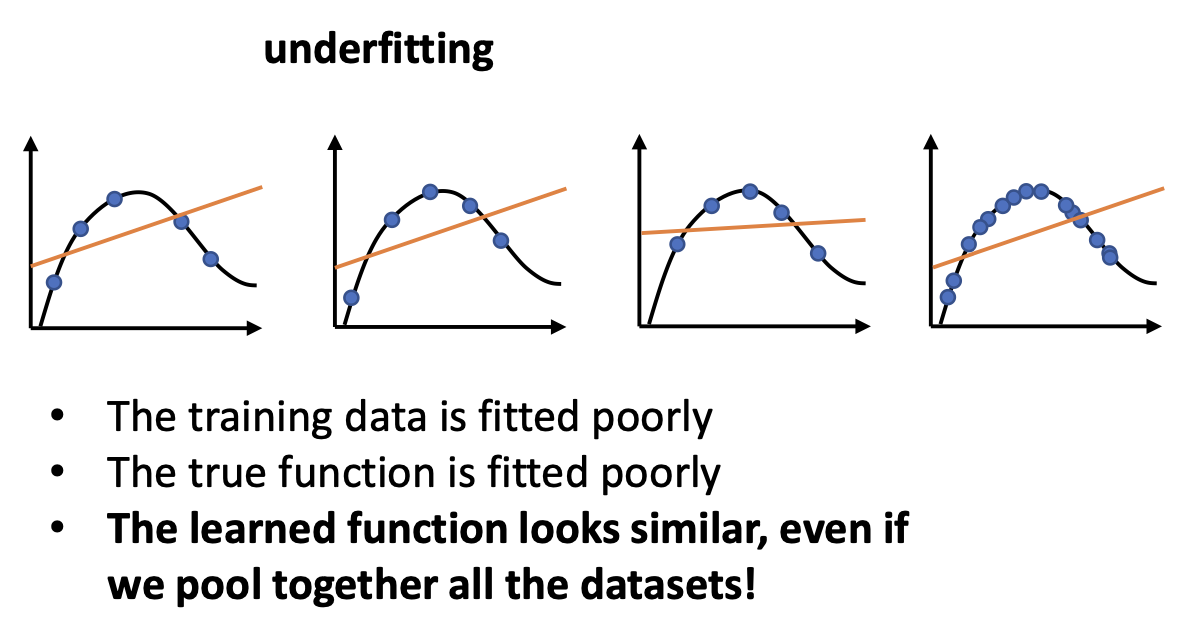
그리하여, underfitting일 때는 training set이 변하더라도 우리의 function output은 큰 변화가 없을 것이다.
Let's analyze error
Overfitting과 underfitting을 이루는 요소들을 알아보기 위해 error를 분석하고자 한다.
Error는 어떤 내용을 담고 있을까?
그에 대해 알아보기 위해 아래의 질문에 대해 먼저 생각해보자.
Q. 가능한 데이터셋들의 분포가 주어질 때, error의 기대값은 어떻게 구할 수 있을까?
우리에게 주어진 데이터셋 D에 대해서는 그 분포를 확인할 수 있다.
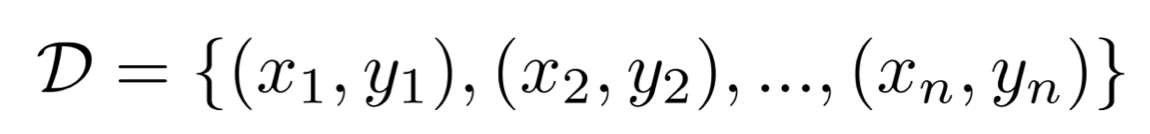
데이터셋 D가 위와 같은 구성으로 주어졌을 때, 모든 data pair들이 i.i.d. 가정을 따른다면, 우리는 아래와 같이 데이터셋 D가 샘플링될 확률을 구할 수 있다.
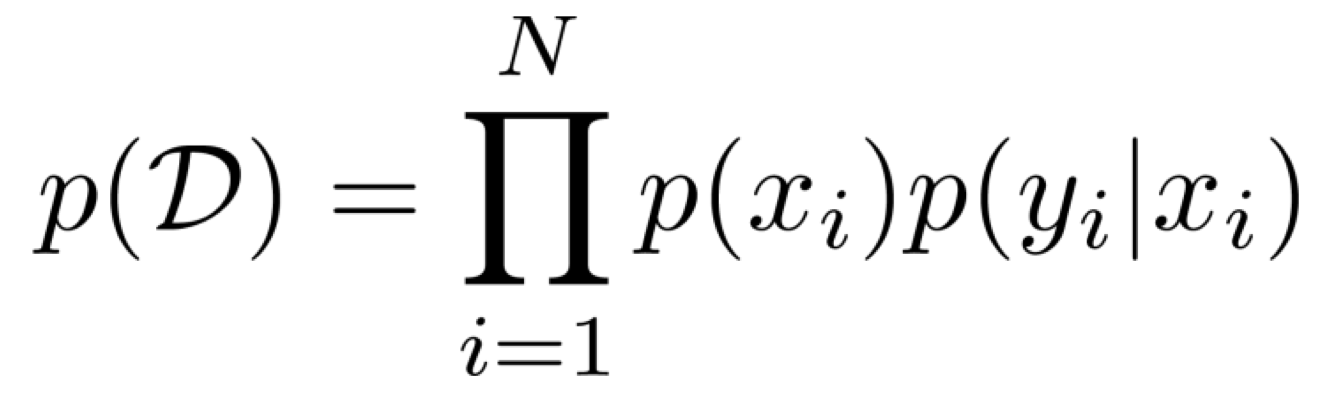
이때, 우리는 어떻게 기대값 loss를 구할 수 있을까?
우리의 loss function은 위에서 아래와 같이 정의되었다.
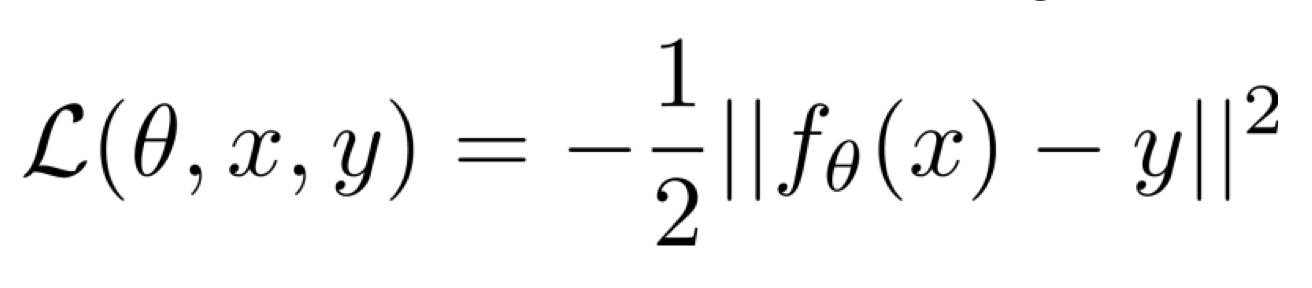
지금 우리는 샘플링된 데이터셋 D를 통해 얻을 수 있는 기대값 loss를 구하려고 하고 있다.
그렇기 때문에 notation을 조금 수정하려고 한다.
우리 모델의 예측을 나타내는 $f_\theta(x)$를 $f_D(x)$로 수정한다. 의미는 같으나, 데이터셋 D가 샘플링 되어 만들어진 예측임을 강조하기 위함이다.
다음으로, label 값을 나타냈던 y를 $f(x)$로 나타낸다. $f(x)$는 true function을 나타낸다. 결국, label과 일맥상통한다.
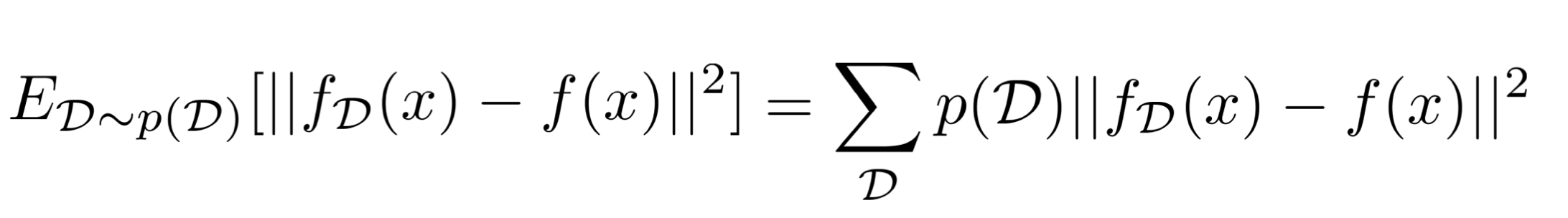
그렇다면 위와 같이 샘플링된 데이터셋 D를 통해 얻을 수 있는 기대값 loss를 구할 수 있게 된다.
굳이 이렇게 정의한 이유는, 우리의 알고리즘이 어떤 특정한 데이터셋에 의해 overfitting 되거나 underfitting 되는 것이 아닌, 데이터와는 독립적으로 어떤 결과를 내는지 확인해보기 위해서 샘플링된 데이터셋 D로 수정하여 loss function을 변경했다.
따라서, 이제 우리가 방금 정의한 loss function의 값은 어떤 특정한 데이터셋으로부터 얻을 수 있는 값이 아닌, 데이터의 생김새와는 독립적으로 우리의 알고리즘의 성능에 의해 얻을 수 있게 되는 loss function 값이라고 할 수 있다.
이제 overfitting과 underfitting을 이루는 요소들을 파악해보기 위해, 위의 loss function으로부터 나오는 error를 분석해보려고 한다.
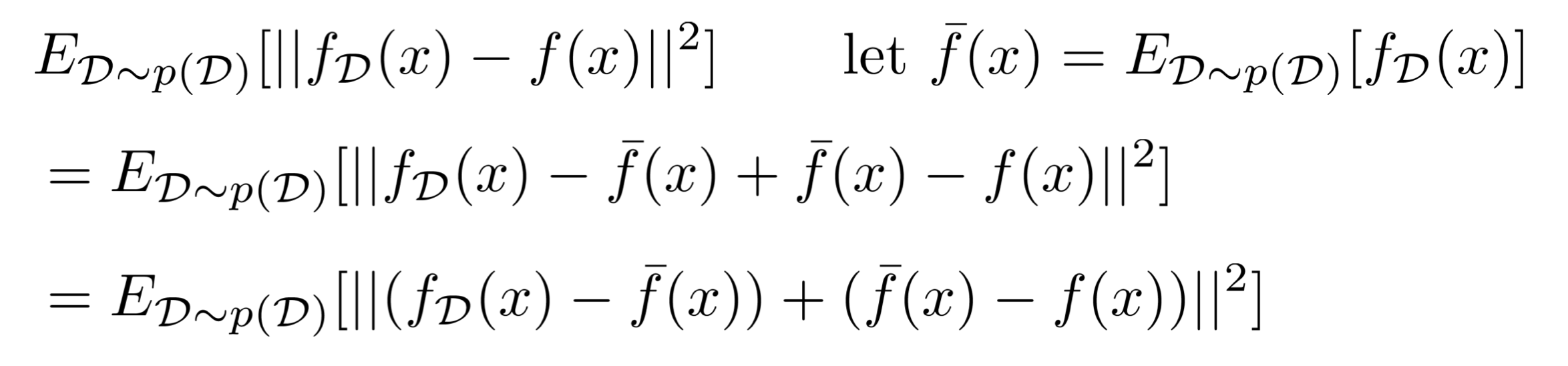
$\overline{f}(x)$를 위와 같이 정의했을 때, 우리는 다음과 같이 전개할 수 있다.
1. 정의했던 loss function에 -$\overline{f}(x)$와 +$\overline{f}(x)$를 넣어준다.
2. + 부호를 기준으로 양쪽을 괄호로 감싼다.
그러면, 우리는 이 식을 $(x - y)^2$이라는 식으로 생각하고 $x^2 - 2xy + y^2$ 형태로 풀 수 있게 된다.
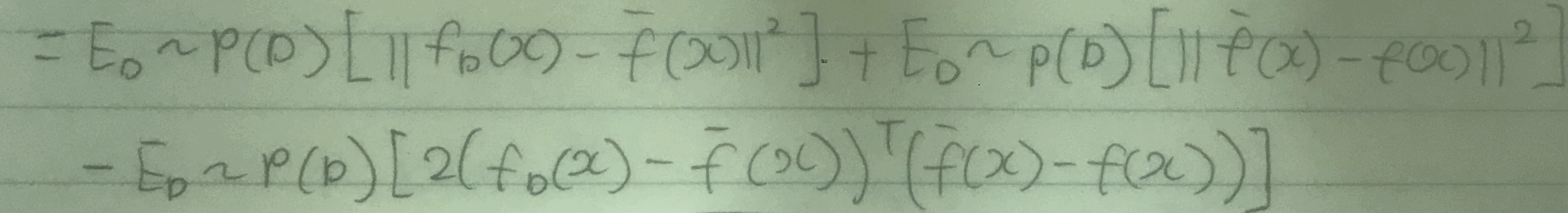
이렇게 전개를 하면 없앨 수 있는 항이 만들어진다.
그것은 바로 3번째 항이다. 우리가 가정해서 사용하고 있는 $\overline{f}(x)$는 $f_D(x)$와 같다.
따라서, 둘의 마이너스 결과는 0이 되므로 3번째 항 전체가 사라진다.
그러면 아래와 같이 2개의 항만이 남게 된다.
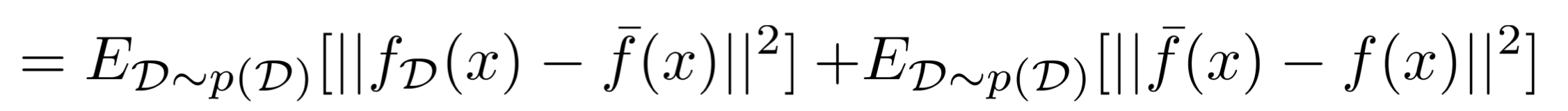
* 첫 번째 항은 지워지지 않는 이유
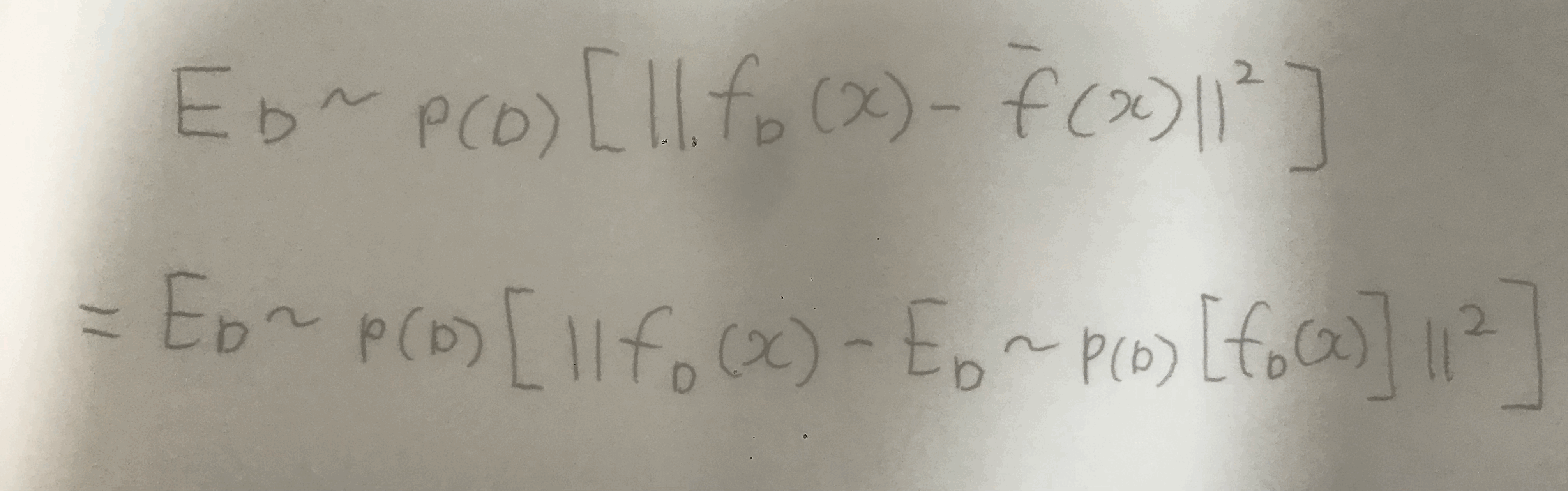
Variance
위의 2개 항은 각각 의미를 지니고 있다.
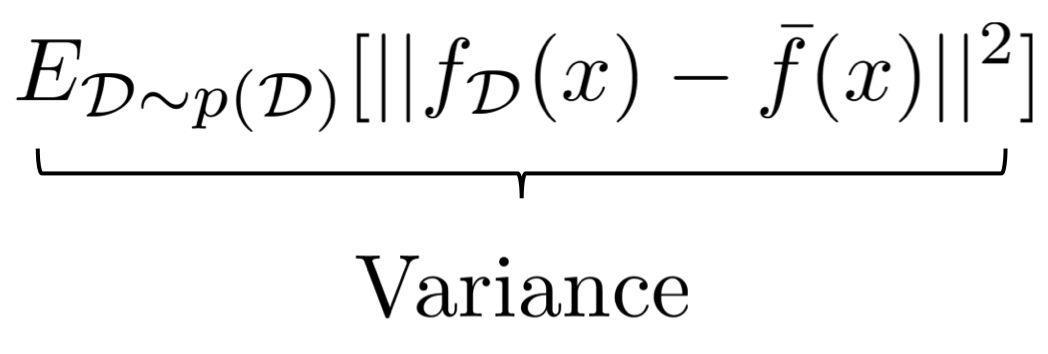
첫 번째 항은 variance를 의미한다.
variance란 true function과는 상관 없이, 데이터셋에 따라 모델의 예측이 변하는 정도를 나타낸다.
Bias

두 번째 항은 bias를 의미한다. (두 번째 항은 데이터셋 D가 샘플링될 확률과 연관이 없으므로 기대값을 제거할 수 있다.)
bias는 위의 식 그대로 예측의 평균값과 정답값의 거리를 나타낸다. 따라서, bias가 높으면 예측 평균값과 정답값의 차이가 큰 것이다.
따라서, bias는 얼마나 underparameterized 되어 있는지 확인할 수 있도록 한다.
우리의 loss function의 값은 아래와 같이 나타낼 수 있었다.
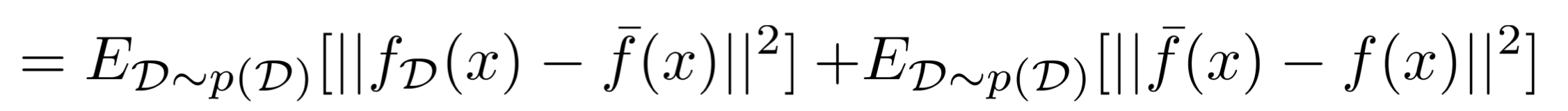
그리고 첫 번째 항은 variance, 두 번째 항은 bias였기에 loss function의 총 loss 값은 아래와 같이 구성된다고 할 수 있다.
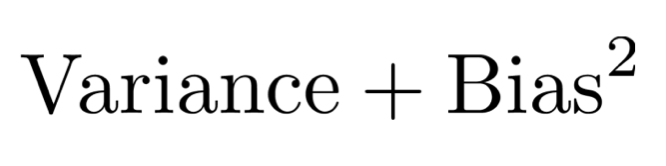
Bias-variance tradeoff
따라서, overfitting과 underfitting은 variance와 bias의 tradeoff로 인해 이루어진 결과라고 할 수 있다.
만약 variance가 높다면, true function과는 별개로 데이터셋에 따른 변화도가 높다는 의미이므로 overfitting이 발생한다.
만약 bias가 높다면, underparameterized가 되었다는 의미이므로 underfitting이 발생한다.
그러므로 적당한 variance, bias가 나타난다면 overfitting과 underfitting 문제를 해결할 수 있을 것이다.
* 우리는 bias가 높은 상황은 학습 중에 인지할 수 있지만, variance가 높은지는 학습 중에 알 수 없다.
-> bias가 높을 때는 train loss가 높을 때라고 말할 수 있지만, train loss가 낮을 때 variance가 높다고 말할 수는 없다. train loss가 낮다고 무조건 overfitting이 발생하지는 않기 때문이다.
References
'자연어 처리 과정' 카테고리의 다른 글
| Backpropagation (0) | 2023.07.31 |
|---|---|
| Regularization (0) | 2023.07.26 |
| Logistic regression (0) | 2023.07.23 |
| Perceptron algorithm (0) | 2023.07.23 |
| Eigenvector, eigenvalue 그리고 diagonal과 eigendecomposition (0) | 2023.07.08 |



