개요
우리의 데이터를 zero-mean, unit-variance로 만들어주는 normalization 기법 중
Batch normalization이 무엇인지 알아보자.
왜 zero-mean과 unit-variance?
우리에게는 여러 가지 normalization 방법들이 존재한다.
z-score, minmax, batch normalization 등
이 중 minmax를 제외하고는 normalization을 거침으로써 데이터들의 평균을 0, 분산을 1로 만들어준다.
왜 하필 데이터들의 평균을 0, 분산을 1로 만들어주는 것일까?
그 이유는 normalization을 하고 나서 통과할 함수인 activation function을 보면 알 수 있다.

maxout activation function을 제외하고 보자.
모두 non-linear하게 데이터들을 activation 시켜주는 함수들이다.
우리는 데이터들을 normalization을 하고 나서 activation function에 통과시킬 것이다.
그 말인 즉, activation function에 우리의 데이터들을 뿌릴 예정이라는 거다.
이때 신경써야하는 점이 무엇인가?
그것은 바로 gradient vanishing(saturated), non-linearity의 유지이다.
그러니까 되도록이면 데이터가 activation function에 뿌려질 때 기왕이면 그래프의 가운데 정도에 뿌려져야
gradient vanishing도 안 되고, non-linearity도 유지가 되는 것이다.

만약, 위처럼 평균이 0인 위치에 데이터가 있지 않고 0보다 큰 위치에 뿌려졌다면
linear하게 되어버린다.
(빨간색 부분에만 데이터가 있으면 선형 변환과 다를 게 없기 때문에)
즉, ReLU의 output인 max(0, x)로 activation 될 수가 없다.
그런데 저 그래프의 가운데에 뿌리려고 봤더니 값이 평균은 0, 분산은 1정도였다는 것이다.
그래서 zero-mean, unit-variance로 데이터를 normalization 해주는 것이다.
activation function에 정상적으로 통과가 되어야 layer를 제대로 쌓을 수 있으니까!
그렇다면 Batch normalization이란?
우선 batch는 데이터가 모여있는 주머니라고 생각하면 된다.
데이터가 100개가 있고 batch size = 10이라면,
주머니 10개에 100개의 데이터를 나눠서 담는 것이다.
그럼 한 주머니에 10개씩 데이터가 담길 것이다.
normalization의 목적은 데이터를 평균 0, 분산 1로 맞춰주는 것이다.
우리의 데이터는 batch에 담겨 있으니, batch 그 자체를 평균 0, 분산 1로 맞춰주면 batch normalization이 되는 것이다.
그리고 batch normalization은 두 단계로 이뤄져 있다. 즉, normalization 해주는 것만이 다가 아니다.
아래의 단계로 batch normalization이 이루어진다.
1. normalize
2. scale and shift
1. Normalization
우선 첫 번째 단계를 하려면, batch 한 개에 담긴 모든 데이터들을 탐색하여 값을 더해주고 그것으로 평균을 구하고 분산을 구해주면 된다.

normalize 단계에서 보이는 것처럼 해당 배치 안에 있는 i번째 데이터에서 해당 배치의 평균을 빼준다.
그리고 그것을 표준편차로 나눠주는 것이다. 분산 옆에 더해진 것은 분산이 0이 되는 것을 막기 위한 입실론이다.
이렇게 각 배치마다 normalization을 해주면 모든 배치가 평균 0, 분산 1이 되는 것이다!
2. Scale and shift
위에 있는 사진에서 볼 수 있듯이, batch normalization된 결과물인 y는 x에 감마와 베타가 곱해진 후에 도출된다.
기껏 batch 데이터를 평균 0, 분산 1로 만들었는데 그 데이터에 왜 또 감마와 베타를 곱해주는 걸까?
우선, 감마와 베타는 우리가 초깃값만 정해주면 학습 과정에서 알아서 update가 되는 parameter이다.
초깃값은 감마는 0, 베타는 1로 설정한다.
어디서 많이 본 숫자이다.
즉, 감마는 평균과 비슷하다고 보면 되고 베타는 분산과 비슷하다고 보면 된다.
평균은 x축에서 데이터들을 얼마나 왼쪽으로 혹은 오른쪽으로 위치시킬지 결정해주고(데이터들을 위치시킬 좌표 역할)
분산은 데이터들을 얼마나 넓게 포진시킬지 결정해준다.
그럼 이게 무슨 말이냐?
데이터를 애써서 가운데에 평균 0, 분산 1자리에 모아놨는데 이 데이터들을 다시 scale 해주고 shift(이동)시켜준다는 것이다.
그러니까 왜?
꼭 평균 0, 분산 1에 데이터가 모여있는 게 언제나 좋은 건 아니기 때문이다!
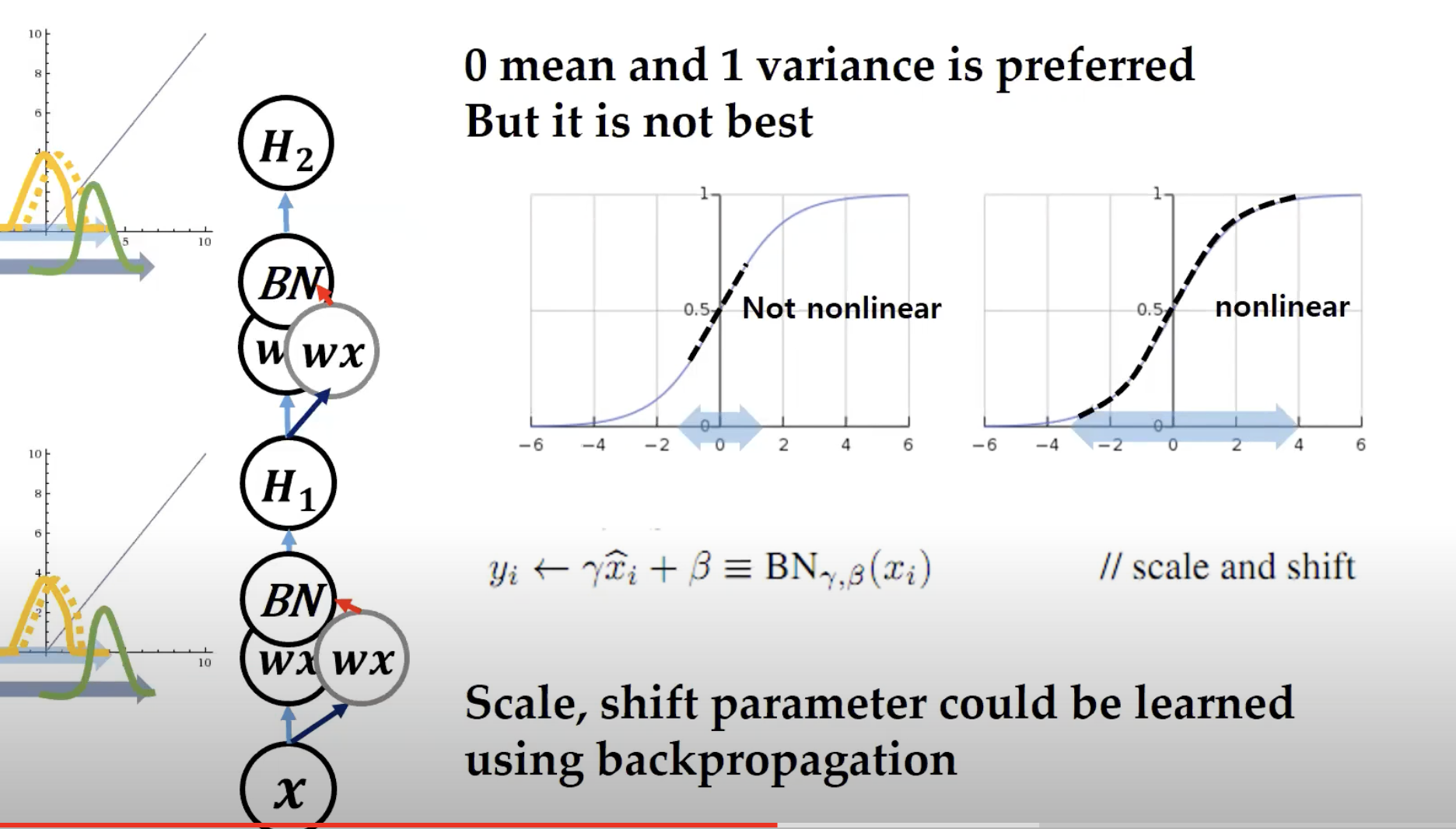
sigmoid function에 넣기 전에 데이터들을 zero-mean, unit-variance로 만들어놨더니
데이터들이 선형 변환을 하게 되는 모습을 볼 수 있다.
즉, sigmoid가 non-linearity를 잃어버리는 모습을 확인할 수 있다.
이런 문제가 발생하기 때문에, 컴퓨터가 학습을 진행하면서 어느 정도 알아서 최적의 감마, 베타 값을 찾은 다음
우리의 데이터들을 너무 몰려있지는 않게, 적절하게 위치시켜주는 것이다!
여기서 생기는 의문점
1. 알아서 감마와 베타를 조정해서 데이터를 분포시켰다고 해도
normalization은 activation하기 전에 이뤄지는 것이기 때문에
vanishing gradient와 non-linearity를 잃어버리는 문제가 발생할 수 있지 않나?
그렇다.
하지만, activation function을 통과시킨 후에 다시 normalization을 해주면 되기 때문에 상관이 없는 것이다.
즉, 데이터가 아무리 넓게 퍼져있거나 아무리 좁게 모여있어도 다시 normalization layer를 넣어주면 되는 것이다.
2. test data는 batch 데이터가 아닌데 어떻게 평균과 분산을 구해서 batch normalization을 하는지?
만약, 우리에게 10개의 batch가 있다고 하면 그 10개의 batch의 평균값을 모두 기록해놓은 다음 그 값을 가지고 계산하는 것이다.
테스트 데이터의 평균값 = 지금까지 배치들의 모든 평균값을 더한 것을 batch size로 나눈 값
테스트 데이터의 분산값 = 지금까지 배치들의 모든 분산값을 더한 것을 batch size로 나눈 값
그런데 이렇게 하면 생기는 문제가 하나 있다.
batch에서 계산한 값들을 모두 저장하는 것에 있어 메모리의 부담이 있다는 것이다.
따라서, test data에 대해서는 근사값으로 설정을 한다.
learning average와 moving average를 설정해서 현재와 이전 값을 얼마나 신뢰할 것인지 판단하여
테스트 데이터를 위한 평균과 분산값을 계산한다!
'자연어 처리 과정' 카테고리의 다른 글
| CNN의 연산 (0) | 2022.12.18 |
|---|---|
| AlexNet (0) | 2022.12.18 |
| Overfitting과 underfitting 그리고 regularization (0) | 2022.12.01 |
| Softmax function and cross-entropy loss (0) | 2022.11.30 |
| Cost function for Logistic regression (1) | 2022.11.30 |



