역행렬이 존재하는지 판단하기 위해서 사용했던 det()
이 det은 determinant의 줄임말이다.
determinant는 linear transformation을 위해 A에 입력벡터를 통과시켰을 때
얼마나 변화했는지의 정도를 나타내준다.
크게 두 가지를 보면 된다.
1. 어떠한 input이 matrix A를 통과하게 되면 부피(volume)이 얼마나 변하는가?
2. 어떠한 input이 matrix A를 통과하게 되면 방향(orientation)이 변하는가?
첫째로, 부피 차원에서 살펴보자.

[1, 0], [0, 1]이라는 벡터 i, j로 만들어진 그래프가 있다고 하자.
이 벡터를 [[2, 0], [0, 2]]라는 matrix A에 통과시켜보도록 하겠다.
그럼 아래와 같이 벡터가 변하게 된다.

matrix A는 diagonal matrix였기 때문에 i, j를 각각 2배로 resize해주었다.
따라서 넓이는 원래 1이었다가 현재 4가 된 상태이다.
이제 diagonal matrix였던 matrix A의 det을 한번 구해보자

det의 결과값으로는 4가 나오게 된다.
넓이가 1에서 4로 4배가 됐는데, 이 수치와 det(A)의 값이 같다.
즉 det은 linear transformation이 얼마나 변하게 하냐는 정도를 나타내 준다고 했으므로
그 정도는 det(A)를 하면 알 수 있는 것이다!
둘째로, 방향(orientation) 차원에서 살펴보자.
알아보기 위해 이번에는 통과시킬 matrix A를 [[-2, 0], [0, 2]라고 해보자.
그렇다면 i와 j는 아래와 같이 linear transformation을 겪게 된다.

위에서의 예와 같이 i와 j는 각각 두 배씩 늘어났다.
그래서 위에서와 동일하게 determinant의 절대값은 동일하게 4가 나와야 한다.
구해보자.
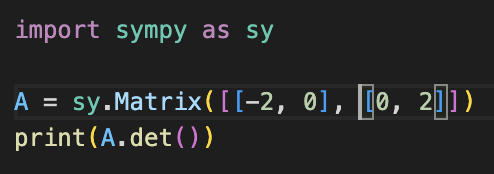
완전히 동일한 값이 나오지는 않았다.
이번에는 -4가 나왔다.
절대값은 4이나 앞에 -(마이너스) 부호가 붙어서 나왔다.
왜?
방향이 바뀌었기 때문이다.
즉, A를 통과시킴으로써 방향(orientation)을 보존하지 못했다는 의미이다!
마무리
이와 같이 determinant의 절대값은 linear transformatioin 후에 변화하는 부피의 정도, 방향의 변화 여부를 알려준다!
'Hacks' 카테고리의 다른 글
| 약수 찾기 알고리즘 (1) | 2022.11.19 |
|---|---|
| cosΘ = np.dot(a, b) = ||a|| * ||b|| * cosΘ (0) | 2022.11.17 |
| 다중집합 (0) | 2022.11.15 |
| 위상정렬 (0) | 2022.11.14 |
| 파이썬에서 csv 파일에 데이터를 쓰고, 읽어오기 (0) | 2022.11.11 |
