Matrix A(m x n)

Set builder notation

Row space A
A set of linear combination Ax, when every vector x is in m-dimension.

Column space A
A set of linear combination Ax, when every vector x is in n-dimension.

Null space A
A set of vector x, which makes linear combination Ax to zero vector.

* Null space A is perpendicular to Row space A
Left null space A
A set of vector y, which makes linear combination A^Ty to zero vector.
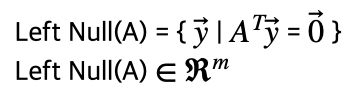
* Left null space A is perpendicular to Column space A
For more
https://angeloyeo.github.io/2020/11/17/four_fundamental_subspaces_en.html
Relationship of Four Fundamental Subspaces - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
http://mlwiki.org/index.php/Four_Fundamental_Subspaces
Four Fundamental Subspaces - ML Wiki
Four Fundamental Subspaces A matrix $A$ has four subspaces: Column Space $C(A)$ or $\text{ran}(A)$: Range of $A$ Nullspace $N(A)$ or $\text{null}(A)$ Row Space $C(A^T)$ of $A$ is the same as Column Space of $A^T$ Nullspace of $A^T$ (also called "Left Nulls
mlwiki.org
[Linear Algebra] Lecture 10 네 개의 주요 부분 공간(Fundamental subspaces)
1. 네 개의 주요 부분 공간(Four fundamental subspaces) 이번 포스팅에선 행렬 A에 대한 네 개의 주요 부분 공간(Fundamental subspaces)에 대해 다뤄보겠다. 이들 주요부분공간 각각에 대해 알아보고 이들이 서
twlab.tistory.com
References
https://www.mathbootcamps.com/column-space-matrix/
The column space of a matrix - MathBootCamps
The column space of a matrix is the span, or all possible linear combinations, of its columns. Let’s look at some examples of column spaces and what vectors are in the column space of a matrix. Note that since it is the span of a set of vectors, the colu
www.mathbootcamps.com


